Тем не менее, Равновесие все еще может иметь различные качественные особенности. В примере выше  и
и 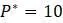 являются равновесиями, но популяция, близкая к 0, имеет тенденцию отходить от 0, тогда как популяция близкая к 10 имеет тенденцию двигаться к 10. Таким образом, 0 является неустойчивым или отталкивающим равновесием, а 10 является стабильным или притягивающим равновесием.
являются равновесиями, но популяция, близкая к 0, имеет тенденцию отходить от 0, тогда как популяция близкая к 10 имеет тенденцию двигаться к 10. Таким образом, 0 является неустойчивым или отталкивающим равновесием, а 10 является стабильным или притягивающим равновесием.
Предположим, что модель близка к описанию реальной популяции, стабильные равновесия – это те, которые можно наблюдать не только в живой природе. Поскольку любая система, вероятно, будет иметь небольшие отклонения от идеальной модели, даже когда популяция находится в состоянии равновесия, ожидается, что она будет меняться, по крайней мере, благодаря тем факторам, которые исключены из модели или изначально не принимались во внимание. Однако, отклоняясь на небольшое расстояние от стабильного равновесия, наблюдаемое значение будет возвращаться к нему обратно. С другой стороны, если происходит отклонение от неустойчивого равновесия, то наблюдаемое значение остается в стороне. Хотя нестабильные равновесия важны для понимания модели в целом, они не являются характерными особенностями популяции, которые стоит когда-либо ожидать в реальном мире.
Далее займёмся вопросами линеаризации. Следующая цель – определить, что заставляет одни равновесия быть стабильными, а другие – нестабильными.
Стабильность зависит от того, что происходит вблизи равновесия. Итак, чтобы сконцентрироваться в окрестности 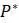 , рассмотрим популяцию
, рассмотрим популяцию 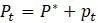 , где
, где 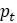 – очень маленькое число, которое говорит о том, насколько далеко популяция находится от состояния равновесия. Называется
– очень маленькое число, которое говорит о том, насколько далеко популяция находится от состояния равновесия. Называется 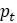 отклонением от равновесия и интересно тем, как оно меняется с течением времени. Вычислим
отклонением от равновесия и интересно тем, как оно меняется с течением времени. Вычислим 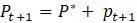 и используем его для поиска
и используем его для поиска 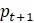 . Если
. Если 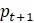 больше, чем
больше, чем 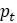 по абсолютной величине, то можно сделать вывод о том, что
по абсолютной величине, то можно сделать вывод о том, что 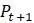 отдалилось от
отдалилось от 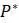 . Если наоборот,
. Если наоборот, 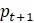 меньше
меньше 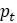 по абсолютной величине, то
по абсолютной величине, то 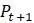 приблизилось к
приблизилось к 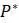 . Если теперь проанализировать, как меняется
. Если теперь проанализировать, как меняется 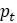 на всех достаточно малых значениях
на всех достаточно малых значениях 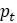 , то можно будет определить, является ли исследуемое равновесие стабильным или нестабильным. Растущее отклонение означает нестабильность, в то время как уменьшающееся означает стабилизацию. Здесь не учитывается знак отклонения, рассматривая лишь абсолютное значение. Знак стоит принимать во внимание в последнюю очередь, так как он не имеет прямого отношения к вопросу о стабильности.
, то можно будет определить, является ли исследуемое равновесие стабильным или нестабильным. Растущее отклонение означает нестабильность, в то время как уменьшающееся означает стабилизацию. Здесь не учитывается знак отклонения, рассматривая лишь абсолютное значение. Знак стоит принимать во внимание в последнюю очередь, так как он не имеет прямого отношения к вопросу о стабильности.
Пример. Рассмотрим модель 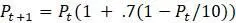 , с которой уже сталкивались ранее и знаем, что равновесие достигается в точках
, с которой уже сталкивались ранее и знаем, что равновесие достигается в точках 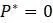 и 10. В первую очередь исследуем
и 10. В первую очередь исследуем 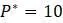 , которое, судя по графику, стабилен на основании численных экспериментов. Подстановка значений
, которое, судя по графику, стабилен на основании численных экспериментов. Подстановка значений 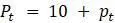 и
и 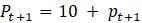 в уравнение для модели приводит к следующему выводу:
в уравнение для модели приводит к следующему выводу:
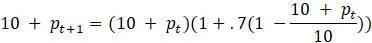
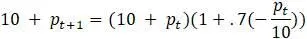
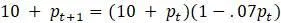
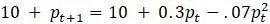
Заметим, что 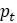 является очень малым числом, меньше 1, следовательно,
является очень малым числом, меньше 1, следовательно, 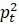 еще меньше и ничтожно мало по сравнению с
еще меньше и ничтожно мало по сравнению с 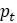 . Таким образом
. Таким образом 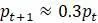 .
.
Читать дальше

 и
и 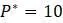 являются равновесиями, но популяция, близкая к 0, имеет тенденцию отходить от 0, тогда как популяция близкая к 10 имеет тенденцию двигаться к 10. Таким образом, 0 является неустойчивым или отталкивающим равновесием, а 10 является стабильным или притягивающим равновесием.
являются равновесиями, но популяция, близкая к 0, имеет тенденцию отходить от 0, тогда как популяция близкая к 10 имеет тенденцию двигаться к 10. Таким образом, 0 является неустойчивым или отталкивающим равновесием, а 10 является стабильным или притягивающим равновесием.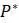 , рассмотрим популяцию
, рассмотрим популяцию 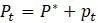 , где
, где 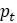 – очень маленькое число, которое говорит о том, насколько далеко популяция находится от состояния равновесия. Называется
– очень маленькое число, которое говорит о том, насколько далеко популяция находится от состояния равновесия. Называется 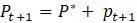 и используем его для поиска
и используем его для поиска 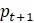 . Если
. Если 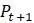 отдалилось от
отдалилось от 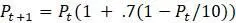 , с которой уже сталкивались ранее и знаем, что равновесие достигается в точках
, с которой уже сталкивались ранее и знаем, что равновесие достигается в точках 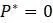 и 10. В первую очередь исследуем
и 10. В первую очередь исследуем 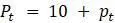 и
и 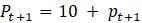 в уравнение для модели приводит к следующему выводу:
в уравнение для модели приводит к следующему выводу: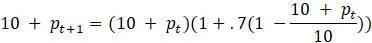
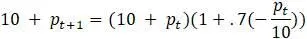
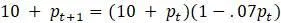
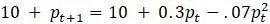
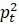 еще меньше и ничтожно мало по сравнению с
еще меньше и ничтожно мало по сравнению с 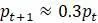 .
.










