Денис Соломатин - Математические модели в естественнонаучном образовании. Том I

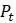Это означает, что значения близкие к равновесию будут иметь отклонение от равновесия, уменьшающееся примерно в 0.3 раза с каждым последующим шагом времени. Поэтому небольшие отклонение от равновесия в дальнейшем уменьшаются и 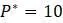действительно стабильное значение.

Можно смотреть на число 0.3 как на «коэффициент растяжения», который говорит о том, насколько стремительно меняются отклонения от равновесия с течением времени. В данном примере, поскольку растягиваемся в менее чем 1 раз, на деле имеет место сжатие.

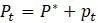Процесс, описанный в примере выше, называется линеаризацией модели в равновесии, потому что сначала фокусируем внимание вблизи равновесия путем линейной замены , а затем игнорируем члены степени больше 1 в 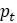. Остается только линейная модель, аппроксимирующая исходную модель. Линейные модели, как видели, легко понять, потому что они производят либо экспоненциальный рост, либо распад.

Вопросы для самопроверки:

– Выполните аналогичный анализ для другого равновесия этой модели, чтобы показать, что оно нестабильно. Каким будет коэффициент растяжения, на который расстояния от точки равновесия растут с каждым шагом времени?

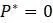В результате аналогичного анализа в окрестности 0 обнаружится, что линеаризация при дает 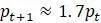. Поэтому возмущения от этого равновесия со временем растут, следовательно, неустойчиво. В общем случае, когда коэффициент растяжения больше 1 по абсолютной величине, равновесие нестабильно. И наоборот, когда оно меньше 1 по абсолютной величине, равновесие стабильно.

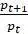Из курса математического анализа известно, что вышеописанный процесс линеаризации напоминает аппроксимацию графика функции по касательной прямой. Развивая эту идею коэффициент растяжения в предыдущем примере можно было бы выразить как отношение при бесконечно малых значениях 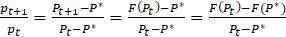. Но , где 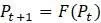уравнение, определяющее модель. Заметим, что в последнем равносильном преобразовании использовалось равенство 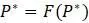. Поскольку интересны лишь значения 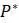, очень близкие к , то последнее выражение очень близко к предельному значению 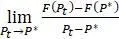. Но этот предел по определению является не чем иным, как производной 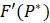, производной функции, определяющей модель. Итак, мы доказали следующую теорему.

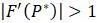Теорема. Если модель имеет равновесное значение , то подразумевает, что значение 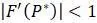нестабильно, а при , будет 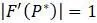стабильным значением. Если же , то этой информации недостаточно для определения стабильности и необходимо проводить дополнительное исследование.