Подобный «хаос» в действительности имеет довольно точное техническое определение, но не будем его приводить. Вместо этого просто неформально укажем на два требования, которые математики предъявляют к употреблению этого слова: 1) модель должна быть детерминированной, то есть в ней не может быть случайности; и 2) прогнозы модели чрезвычайно чувствительны к начальным условиям.
Чтобы увидеть, как именно дискретная логистическая модель проявляет свою хаотичность, например, зафиксировав 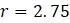 , достаточно проиллюстрировать проявление второго требования. На рисунке 1.7 показаны значения
, достаточно проиллюстрировать проявление второго требования. На рисунке 1.7 показаны значения 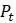 , которые возникают из двух разных, но достаточно близких друг к другу значений
, которые возникают из двух разных, но достаточно близких друг к другу значений 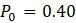 и
и 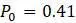 .
.
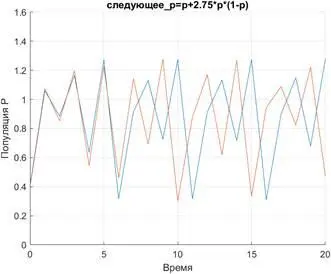
Рисунок 1.7 Результаты роста значения 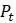 , полученные из двух близких начальных значениях
, полученные из двух близких начальных значениях 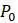 для логистической модели
для логистической модели 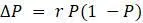 при
при 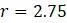 .
.
Обратите внимание на тот факт, что, хотя популяции и изменяются похожим образом в течение нескольких первых шагов, после этого они становятся полностью различимыми. В результате для такой пары значений наблюдается чрезвычайная чувствительность модели к начальным условиям. Конечно, это не является доказательством чего-либо, и вполне возможно, что такое поведение было просто последствием череды ошибок компьютерного округления. Однако математиками строго доказано, что это подлинный «хаос».
Возможность хаотического поведения в такой простой популяционной модели, как дискретная логистическая, вызвала большой ажиотаж в 1970-х годах, когда она была впервые опубликована в работе Мэй от 1978 года. Если бы такая простая модель смогла воспроизводить сложное поведение любой динамической системы, то от гипотезы о том, что сложная динамическая система может возникать лишь из сложных взаимодействий и флуктуаций окружающей среды пришлось бы отказаться. Дальнейшая работа Мэй с сотоварищами по вычислению соответствующих значений таких параметров, как 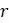 , в математических моделях на основании лабораторных и реальных популяциях насекомых заставила их усомниться в том, что хаотическое поведение действительно наблюдается в реальной динамике живых популяций. Тем не менее, исследование эпидемий кори в Нью-Йорке действительно предполагало возможность контролируемого хаоса. Однако эпидемический паротит и ветряная оспа, как оказалось, вели себя отнюдь не хаотично. Хотя та работа все еще не теряет актуальности, существует очень мало данных высокого качества и достаточно длительной продолжительности, чтобы в действительности проверить ключевую идею. В последнее время основное внимание уделялось демографическим моделям, более сложным, чем логистические. Фактически, в 1996 году Кушинг и др. объявили о первом открытии реальной популяции, лабораторной популяции мучного жука триболия, которая демонстрировала хаотическую динамику и опубликовали этот результат в 2001 году.
, в математических моделях на основании лабораторных и реальных популяциях насекомых заставила их усомниться в том, что хаотическое поведение действительно наблюдается в реальной динамике живых популяций. Тем не менее, исследование эпидемий кори в Нью-Йорке действительно предполагало возможность контролируемого хаоса. Однако эпидемический паротит и ветряная оспа, как оказалось, вели себя отнюдь не хаотично. Хотя та работа все еще не теряет актуальности, существует очень мало данных высокого качества и достаточно длительной продолжительности, чтобы в действительности проверить ключевую идею. В последнее время основное внимание уделялось демографическим моделям, более сложным, чем логистические. Фактически, в 1996 году Кушинг и др. объявили о первом открытии реальной популяции, лабораторной популяции мучного жука триболия, которая демонстрировала хаотическую динамику и опубликовали этот результат в 2001 году.
Задачи для самостоятельного решения:
1.3.1. Точки равновесия модели располагаются там, где график зависимости 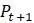 от
от 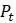 пересекает прямую линию
пересекает прямую линию 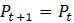 . Предположим, что фокусируемся на участке графика вокруг точки равновесия и увеличиваем масштаб так, чтобы график функции
. Предположим, что фокусируемся на участке графика вокруг точки равновесия и увеличиваем масштаб так, чтобы график функции 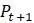 от
от 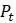 казался прямой линией. В каждой из моделей, показанных на рисунке 1.8, решите, является ли равновесие стабильным или нестабильным, выбрав значение
казался прямой линией. В каждой из моделей, показанных на рисунке 1.8, решите, является ли равновесие стабильным или нестабильным, выбрав значение 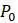 близкое к устойчивому состоянию, а затем изобразите паутинную диаграмму.
близкое к устойчивому состоянию, а затем изобразите паутинную диаграмму.
Читать дальше

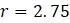 , достаточно проиллюстрировать проявление второго требования. На рисунке 1.7 показаны значения
, достаточно проиллюстрировать проявление второго требования. На рисунке 1.7 показаны значения 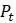 , которые возникают из двух разных, но достаточно близких друг к другу значений
, которые возникают из двух разных, но достаточно близких друг к другу значений 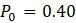 и
и 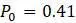 .
.
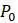 для логистической модели
для логистической модели 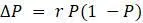 при
при 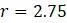 .
.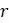 , в математических моделях на основании лабораторных и реальных популяциях насекомых заставила их усомниться в том, что хаотическое поведение действительно наблюдается в реальной динамике живых популяций. Тем не менее, исследование эпидемий кори в Нью-Йорке действительно предполагало возможность контролируемого хаоса. Однако эпидемический паротит и ветряная оспа, как оказалось, вели себя отнюдь не хаотично. Хотя та работа все еще не теряет актуальности, существует очень мало данных высокого качества и достаточно длительной продолжительности, чтобы в действительности проверить ключевую идею. В последнее время основное внимание уделялось демографическим моделям, более сложным, чем логистические. Фактически, в 1996 году Кушинг и др. объявили о первом открытии реальной популяции, лабораторной популяции мучного жука триболия, которая демонстрировала хаотическую динамику и опубликовали этот результат в 2001 году.
, в математических моделях на основании лабораторных и реальных популяциях насекомых заставила их усомниться в том, что хаотическое поведение действительно наблюдается в реальной динамике живых популяций. Тем не менее, исследование эпидемий кори в Нью-Йорке действительно предполагало возможность контролируемого хаоса. Однако эпидемический паротит и ветряная оспа, как оказалось, вели себя отнюдь не хаотично. Хотя та работа все еще не теряет актуальности, существует очень мало данных высокого качества и достаточно длительной продолжительности, чтобы в действительности проверить ключевую идею. В последнее время основное внимание уделялось демографическим моделям, более сложным, чем логистические. Фактически, в 1996 году Кушинг и др. объявили о первом открытии реальной популяции, лабораторной популяции мучного жука триболия, которая демонстрировала хаотическую динамику и опубликовали этот результат в 2001 году.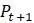 от
от 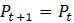 . Предположим, что фокусируемся на участке графика вокруг точки равновесия и увеличиваем масштаб так, чтобы график функции
. Предположим, что фокусируемся на участке графика вокруг точки равновесия и увеличиваем масштаб так, чтобы график функции 










