Денис Соломатин - Математические модели в естественнонаучном образовании. Том I
Здесь есть возможность читать онлайн «Денис Соломатин - Математические модели в естественнонаучном образовании. Том I» — ознакомительный отрывок электронной книги совершенно бесплатно, а после прочтения отрывка купить полную версию. В некоторых случаях можно слушать аудио, скачать через торрент в формате fb2 и присутствует краткое содержание. Год выпуска: 2022, Жанр: Биология, Медицина, Математика, на русском языке. Описание произведения, (предисловие) а так же отзывы посетителей доступны на портале библиотеки ЛибКат.
- Название:Математические модели в естественнонаучном образовании. Том I
- Автор:
- Жанр:
- Год:2022
- ISBN:нет данных
- Рейтинг книги:5 / 5. Голосов: 2
-
Избранное:Добавить в избранное
- Отзывы:
-
Ваша оценка:
Математические модели в естественнонаучном образовании. Том I: краткое содержание, описание и аннотация
Предлагаем к чтению аннотацию, описание, краткое содержание или предисловие (зависит от того, что написал сам автор книги «Математические модели в естественнонаучном образовании. Том I»). Если вы не нашли необходимую информацию о книге — напишите в комментариях, мы постараемся отыскать её.

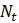 на интервале в 1 год, но описывает численность популяции
на интервале в 1 год, но описывает численность популяции 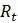 , где приращение t на 1 представляет собой h лет (таким образом,
, где приращение t на 1 представляет собой h лет (таким образом, 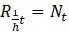 ). Очевидно, что
). Очевидно, что 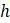 может быть больше или меньше 1; та же формула опишет любую ситуацию.
может быть больше или меньше 1; та же формула опишет любую ситуацию.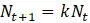 , то модель, описывающая те же популяции с интервалом в 1 год, но использующая приращение времени
, то модель, описывающая те же популяции с интервалом в 1 год, но использующая приращение времени 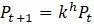 .
.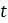 , то пункт (г) показывает, что
, то пункт (г) показывает, что 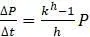 . Если
. Если 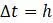 считать бесконечно малым, то получим
считать бесконечно малым, то получим 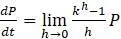 . Проиллюстрировать тот факт, что
. Проиллюстрировать тот факт, что 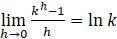 можно выбрав несколько значений
можно выбрав несколько значений 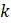 при малом
при малом 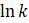 с
с 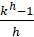 . Этот результат легко доказать формально:
. Этот результат легко доказать формально: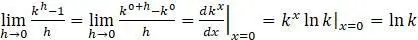
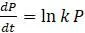 при начальном условии
при начальном условии 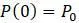 является
является 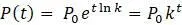 .
.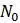 и
и 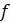 (доля выпускающихся молодых специалистов) и
(доля выпускающихся молодых специалистов) и 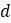 (доля уходящих на заслуженных отдых пенсионеров) для моделируемой численности одинаковы независимо от текущего значения
(доля уходящих на заслуженных отдых пенсионеров) для моделируемой численности одинаковы независимо от текущего значения 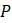 (количество профессиональных математиков работоспособного возраста). На самом деле, когда число
(количество профессиональных математиков работоспособного возраста). На самом деле, когда число 










