Вопросы для самопроверки:
– Какой смысл могут иметь популяции, значения которых не являются целыми числами?
Если измерять размер популяции в единицах, таких как тысячи или миллионы особей, то нет никаких оснований для того, чтобы популяции были целыми числами. Для некоторых видов, таких как коммерчески ценные рыбы, может быть даже целесообразно использовать единицы массы или веса, такие как тонны.
Другая причина, по которой нецелочисленные значения популяции не вызывают опасения, даже если используем поштучные единицы измерения, заключается в том, что пытаемся лишь приблизительно описать размер популяции. Нет ожидания того, что модель даст точные прогнозы. Пока числа невелики, можно просто игнорировать дробные части без значительных потерь.
В таблице 1.5 видим, что популяционное значение увеличивается до пропускной способности 10, как и ожидалось. Сначала это увеличение кажется медленным, затем оно ускоряется, а затем снова замедляется. Построение значений популяции на рисунке 1.2 показывает сигмовидную картину, которая часто появляется в данных тщательно контролируемых лабораторных экспериментов, в которых популяции увеличиваются в ограниченной среде. График показывает значения популяции, связанные сегментами линий, чтобы сделать шаблон более ясным, хотя дискретные временные шаги нашей модели действительно дают популяции только в целочисленное время. Таким образом, с интуитивной точки зрения мы добились определенного прогресса; у нас есть более реалистичная модель для описания роста населения или численности выпускников физико-математических специальностей.
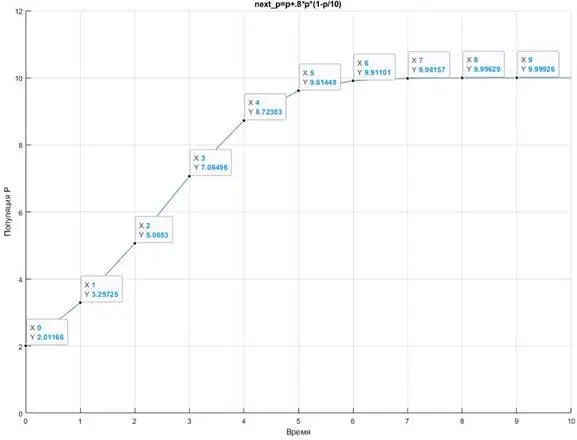
Рисунок 1.2. Популяционные значения из нелинейной модели.
Однако с математической точки зрения не всё так хорошо. В отличие от линейной модели, нет очевидной формулы для 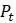 , которая возникала бы из составленной таблицы. На самом деле, единственный способ получить значение
, которая возникала бы из составленной таблицы. На самом деле, единственный способ получить значение 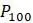 , по-видимому, заключается в создании таблицы с сотней записей в ней. Утратилась легкость, с которой можно было бы предсказывать будущие значения популяции.
, по-видимому, заключается в создании таблицы с сотней записей в ней. Утратилась легкость, с которой можно было бы предсказывать будущие значения популяции.
Это то, с чем приходится мириться: хотя нелинейные модели более реалистичны, зачастую не представляется возможным получение явных формул для решения нелинейных дифференциальных уравнениях. Вместо этого используются графические методы и численные эксперименты для того, чтобы получить общее представление о поведении модели.
Первый из таких методов называется «Паутина». Паутина является основным графическим методом для понимания математической модели дискретного логистического уравнения. Это лучше всего проиллюстрировать на примере.
Рассмотрим еще раз модель 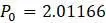 ,
, 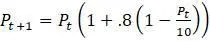 . Начнём с построения графика параболы, определенной уравнением, выражающим
. Начнём с построения графика параболы, определенной уравнением, выражающим 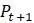 через
через 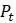 , а также диагональной линии
, а также диагональной линии 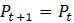 , как показано на рисунке 1.3. Так как популяция начинается с
, как показано на рисунке 1.3. Так как популяция начинается с 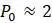 , отмечаем это значение на горизонтальной оси графика. Теперь, чтобы найти
, отмечаем это значение на горизонтальной оси графика. Теперь, чтобы найти 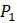 , просто двигаемся вертикально вверх по графику параболы, чтобы найти точку
, просто двигаемся вертикально вверх по графику параболы, чтобы найти точку 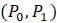 , как показано на рисунке.
, как показано на рисунке.
Далее хотелось бы найти 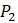 , но для этого нужно отметить
, но для этого нужно отметить 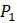 на горизонтальной оси. Самый простой способ сделать это – двигаться горизонтально от точки
на горизонтальной оси. Самый простой способ сделать это – двигаться горизонтально от точки 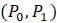 до диагональной линии. Когда достигнем диагональной линии, окажемся в
до диагональной линии. Когда достигнем диагональной линии, окажемся в 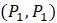 , так как сохранили ту же вторую координату, но изменили первую координату. Теперь, чтобы найти
, так как сохранили ту же вторую координату, но изменили первую координату. Теперь, чтобы найти 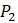 , просто двигаемся вертикально назад к параболе, чтобы найти точку
, просто двигаемся вертикально назад к параболе, чтобы найти точку 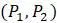 . Теперь это просто вопрос повторения этих шагов навсегда: двигаться вертикально к параболе, затем горизонтально к диагональной линии, затем вертикально к параболе, затем горизонтально к диагональной линии и так далее.
. Теперь это просто вопрос повторения этих шагов навсегда: двигаться вертикально к параболе, затем горизонтально к диагональной линии, затем вертикально к параболе, затем горизонтально к диагональной линии и так далее.
Читать дальше


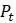 , которая возникала бы из составленной таблицы. На самом деле, единственный способ получить значение
, которая возникала бы из составленной таблицы. На самом деле, единственный способ получить значение 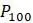 , по-видимому, заключается в создании таблицы с сотней записей в ней. Утратилась легкость, с которой можно было бы предсказывать будущие значения популяции.
, по-видимому, заключается в создании таблицы с сотней записей в ней. Утратилась легкость, с которой можно было бы предсказывать будущие значения популяции.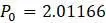 ,
, 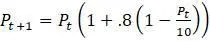 . Начнём с построения графика параболы, определенной уравнением, выражающим
. Начнём с построения графика параболы, определенной уравнением, выражающим 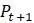 через
через 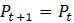 , как показано на рисунке 1.3. Так как популяция начинается с
, как показано на рисунке 1.3. Так как популяция начинается с 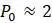 , отмечаем это значение на горизонтальной оси графика. Теперь, чтобы найти
, отмечаем это значение на горизонтальной оси графика. Теперь, чтобы найти 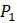 , просто двигаемся вертикально вверх по графику параболы, чтобы найти точку
, просто двигаемся вертикально вверх по графику параболы, чтобы найти точку 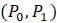 , как показано на рисунке.
, как показано на рисунке.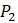 , но для этого нужно отметить
, но для этого нужно отметить 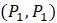 , так как сохранили ту же вторую координату, но изменили первую координату. Теперь, чтобы найти
, так как сохранили ту же вторую координату, но изменили первую координату. Теперь, чтобы найти 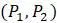 . Теперь это просто вопрос повторения этих шагов навсегда: двигаться вертикально к параболе, затем горизонтально к диагональной линии, затем вертикально к параболе, затем горизонтально к диагональной линии и так далее.
. Теперь это просто вопрос повторения этих шагов навсегда: двигаться вертикально к параболе, затем горизонтально к диагональной линии, затем вертикально к параболе, затем горизонтально к диагональной линии и так далее.










