Денис Соломатин - Математические модели в естественнонаучном образовании. Том I

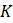Параметры и 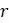в этой модели имеют физические и биологические интерпретации. Во-первых, если 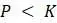, то 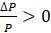. При положительных темпах роста на душу населения население будет увеличиваться. С другой стороны, если 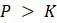, то 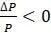. При отрицательных темпах роста на душу населения численность населения будет сокращаться. Поэтому 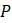называют несущей способностью окружающей среды, потому что она представляет собой максимальное количество особей, которые могут поддерживаться в течение длительного периода. Однако, когда население незначительно (т.е. намного меньше, чем 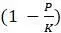), множитель устремляется в 1. Поэтому для малых значений модель аппроксимируется приближенными значениями .

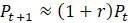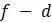Другими словами, играет роль , в вышеописанной линейной модели. Параметр просто отражает то, как популяция будет расти или уменьшаться в отсутствие факторов, зависящих от плотности, когда численность намного ниже предельного значения. Как правило называют конечной внутренней скоростью роста. Термин «внутренний» относится к отсутствию внешнего воздействия, зависящего от плотности, а термин «конечный» подчеркивает тот факту, что используются временные шаги конечного размера, а не бесконечно малые временные шаги дифференциального уравнения.

Вопросы для самопроверки:

– Какие значения можно ожидать от и в случае, когда захотите смоделировать численность ежегодно поступающих на физико-математические факультеты омских ВУЗов?

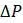Как вы увидите в задачах ниже, существует много способов, которыми разные авторы формируют логистические модели, в зависимости от того, смотрят ли на или 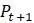, используют ли различные множители. Ключевым моментом, который поможет распознать нелинейную модель, является то, что и 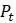, и выражаются как квадратные трехчлены от . Кроме того, эти многочлены не имеют свободного члена (т.е. члена нулевой степени). Таким образом, логистическая модель является простейшей нелинейной моделью, которую можно придумать. Как и в случае с линейной моделью, первым шагом в понимании этой модели является выбор некоторых конкретных значений для параметров 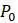и , а также для начальной численности и вычисление следующих значений 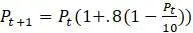. Например, выбирая и так, что и 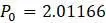, получаем таблицу 1.5.

Таблица 1.5. Популяционные значения из нелинейной модели

t 0 1 2 3 4 5 6 7 8 9 10

2.0117 3.2972 5.0653 7.0650 8.7238 9.6145 9.9110 9.9816 9.9963 9.9993 9.9999