1 > = m;
1> = m — na; <���Р 2> = m + na . (4.11)
Так как генотип всех особей F 1 одинаков, то изменчивость признака в этой популяции обусловлена только влиянием среды, и ее дисперсия равна σ e 2.
Теперь перейдем к популяции F 2, представляющей собой смесь огромного числа (3 n) генотипов. Формулу генотипа каждой особи можно записать как ряд из n аллельных пар со случайной комбинацией сильных и слабых аллелей в каждой паре. Поскольку аллельный состав каждого локуса формируется независимо от остальных, то генотипическая дисперсия популяции F 2 должна представлять собой сумму дисперсий, каждая из которых отражает варьирование у разных особей числа сильных аллелей в каком-то одном локусе. Напомним, что в данной, аддитивной, модели замещение в любом локусе слабого аллеля на сильный ведет к увеличению генотипического значения признака на одну и ту же величину а. Отсюда следует (см. (4.9)), что каждый из n локусов вносит в генотипическую дисперсию поколения F 2 один и тот же вклад а 2 /2. Итак, величину фенотипической дисперсии σ 2в популяции F 2 можно передать формулой
σ 2 = σ e 2 + na 2 /2. (4.12)
Это равенство вместе с другим
<���Р 2> — <���Р 1 > = 2na (4.13)
образует систему двух независимых уравнений, позволяющих определить величину п:
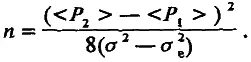 (4.14)
(4.14)
Хотя эта знаменитая формула Кастла — Райта верна лишь в рамках аддитивной модели, она дает возможность ориентировочно подойти к числу генетических факторов, ответственных за межлинейную разницу величины признака.
Что нам дал этот гибридологический экскурс? Очень много. Хотя природные популяции — это не поколение F 2 но и здесь генотипическое значение признака можно считать суммой n независимо варьирующих слагаемых, где n — число локусов в генофонде популяции. Только в отличие от F 2 число аллелей каждого локуса в данном случае может быть больше двух, и в пары они соединяются не в отношении 1:2:1, а по закону Харди — Вайнберга. Хотя мы ничего не знаем ни об эффектах этих аллелей, ни о степени их доминирования, ясно одно: популяционная дисперсия признака должна расти с увеличением числа локусов, принимающих участие в его формировании.
Сигма
Очень часто в качестве меры фенотипической изменчивости используют квадратный корень из дисперсии — так называемое среднеквадратичное отклонение (σ). Для экономии места будем именовать эту величину сигмой , по названию греческой буквы, обычно используемой для ее обозначения. Измеряемая в единицах величины самого признака, сигма очень удобна как масштаб для оценки отклонения величины признака от среднепопуляционного значения. Если признак имеет нормальное распределение, то доля особей с отклонением в пределах одной сигмы составляет 68 %, двух сигм — 95 и трех сигм — 99,7 %. В связи с этим полный размах изменчивости признака, распределенного по нормальному закону, попадает в интервал ±3σ (закон трех сигм). В сигмах принято измерять разность средних значений сравниваемых распределений и, в частности, эффект аллельных замещений.
Как и дисперсия, сигма может служить мерой средовой изменчивости — шума среды. Мы видели, что формула Кастла — Райта позволяет приближенно оценить число локусов, ответственных за различие линий по величине количественного признака. Зная это число, можно определить и средний эффект замещений слабого аллеля на сильный. Очень часто эффект оказывается меньше величины средовой сигмы σ e. Это обстоятельство позволяет почувствовать основную трудность, с которой сталкивается исследователь генетических основ количественных признаков. Ведь если эффект аллельных замещений меньше шума среды, то по фенотипу особи определить ее генотип невозможно. Это же объясняет и гладкий характер распределений по количественным признакам. Шум среды как бы замазывает генотипические различия особей.
При анализе природных популяций широко используется еще одна мера — коэффициент изменчивости признака, т. е. отношение сигмы к среднему значению, выраженное в процентах. Наиболее поразительная черта этого коэффициента заключается в его стабильности при переходе от популяции к популяции в пределах одного вида и даже при сравнении популяций разных видов одного рода. Более того, коэффициент изменчивости самых разных признаков в популяциях эволюционно далеких видов также не слишком различается, несмотря на большие расхождения в величинах средних значений. Отсюда следует, что между сигмой и средним значением существует связь, близкая к прямой пропорциональности. Однако такой вывод в корне противоречит нашему исходному представлению о нормальном характере распределения особей по признаку.
Читать дальше

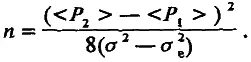 (4.14)
(4.14)







