Владимир Бердников - Эволюция и прогресс

p = (2N 11+ N 12) / 2N = (N 11+ 0,5N 12) / N , (3.2)

q = (2N 22+ N 12) / 2N = (N 22+ 0,5N 12) / N . (3.3)

Гетерозиготы являются донорами сразу двух аллелей, в связи с этим (чисто формально) можно считать, что одна половина гетерозигот вносит в генофонд аллель А 1 , а другая — аллель А 2. Тогда всех особей популяции можно представить в виде суммы двух классов — доноров аллеля А 1 с численностью N 1 и доноров аллеля А 2 с численностью N 2. При этом

N 1= N 11+ 0,5N 12, (3.4)

N 2= N 22+ 0,5N 12. (3.5)

Взглянув на правые части равенств (3.2) и (3.3), мы видим, что в популяции частота каждого аллеля равна доле его доноров:

p = N 1/ N; q = N 2/ N. (3.6)

Рассмотрим популяцию на двух стадиях развития ее особей — на стадии зиготы и взрослого организма. Обозначим численность зигот через N, а численность взрослых — через N'. Каждая из этих величин (N и N') складывается из численностей трех генотипических классов: N 11, N 22, N 12 — для зигот и N 11', N 22', N 12' — для взрослых. Теперь каждому генотипическому классу припишем его приспособленность: w 11— гомозиготам A 1A 1, w 22— гомозиготам А 2А 2 и w 12 — гетерозиготам. Определим приспособленность каждого генотипа как долю зигот (с данным генотипом), достигших взрослой стадии, т. е.

w 11= N' 11/ N 11; w 12= N' 12/ N 12; w 22= N' 22/ N 22 . (3.7)

Так же можно ввести представление и о приспособленности любой группы генотипов. Например, можно говорить о средней приспособленности популяции ( w ) как о доле всех зигот, успешно завершивших развитие. Аналогично определяется средняя приспособленность доноров каждого аллеля — w 1и w 2:

w = N' / N; w 1= N 1' / N 1; w 2= N 2'/ N 2 . (3.8)

Наша главная задача состоит в том, чтобы определить, как под действием отбора изменяется аллельный состав популяции, иначе говоря, как изменяется частота аллелей А 1 и А 2 за время онтогенеза особей.

Доля аллеля в генофонде популяции равна доле его доноров (формулы (3.6)). В случае аллеля А 2 это ( N 2/ N ) — на стадии зигот и ( N 2' / N' ) — на стадии взрослых. Поэтому сдвиг частоты аллеля А 2 в результате отбора ( Δq ) можно получить как разность: ( N 2' / N' ) — ( N 2/ N ). Выразив численности взрослых через численности зигот (см. уравнения (3.8)), получим

Δq = N 2*w 2/ Nw — N 2/ N = q((w 2— w) / w) . (3.9)

Итак, сдвиг частоты аллеля в генофонде популяции в результате отбора равен частоте этого аллеля до отбора, умноженной на относительное превосходство приспособленности его доноров над средней приспособленностью популяции.

Отбор в панмиктической популяции

Перейдем к панмиктической популяции. Здесь при оплодотворении аллели гамет соединяются в генотипы зигот по правилам свободного попарного комбинирования. Зиготы с генотипами А 1А 1, А 1А 2 и возникают в соотношениях р 2: 2pq: q 2 (рис. 10). Эти же соотношения, получившие название закона Харди-Вайнберга, будут справедливы и для взрослых членов популяции, если приспособленность всех генотипов одна и та же. Закон Харди-Вайнберга довольно часто выполняется в природных популяциях, он позволяет легко вычислять частоты генотипов, исходя из частот аллелей.

В нашей модели отличия в приспособленности особей обусловлены только разным уровнем их жизнеспособности, поэтому численности зигот трех генотипических классов А 1А 1, А 1А 2 и А 2А 2 соответственно равны Np 2, 2Npq и Nq 2. Тем самым зиготы в точности отражают генофонд популяции взрослых особей предыдущего поколения. В результате действия отбора численности генотипов взрослых особей, развившихся из зигот, приобретают вид

N 11' = Np 2w 11; N 12' = 2Npqw 12; N 22' = Nq 2w 22 . (3.10)

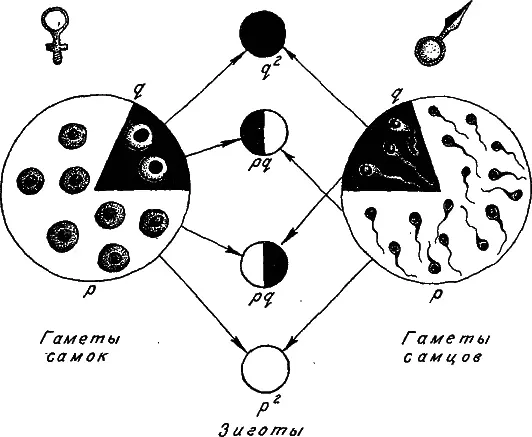
Рис. 10. Схема формирования генотипов зигот при случайном соединении гамет (при панмиксии).

Объяснения в тексте.

Численность всех взрослых особей после отбора связана с численностью зигот уравнением

N' = N(р 2w 11+ 2pqw 12+ q 2w 22). (3.11)

Поскольку отношение N'/N выражает среднюю приспособленность популяции (см. уравнения (3.8)), поделив обе части уравнения (3.11) на N, получим

w = р 2w 11+ 2pqw 12+ q 2w 22 . (3.12)

По аналогии с формулой (3.5) можно получить численность доноров аллеля А 2 после отбора, т. е. среди взрослых потомков

N 2' = N 22' + 0,5N 12' , (3.13)

или, учитывая соотношения (3.10),

N 2' = Nq 2w 22+ Npqw 12 . (3.14)

Поделив обе части этого уравнения на N 2= Nq (см. (3.6)), получим значение приспособленности доноров аллеля А 2 :