Роберт Хайнеманн - Визуальное моделирование электронных схем в PSPICE

Результат просто ошеломляющий. Выясняется, что при изменении уровня импеданса частотного фильтра, то есть если активные и реактивные сопротивления частотного фильтра изменяются на один и тот же коэффициент, частотная характеристика фильтра остается неизменной.

Выполнив задание 1, вы сможете установить, что и переходная характеристика частотного фильтра также не претерпевает никаких изменений, если изменять уровень полного сопротивления.

Задание 8.1.Проведите для схемы фильтра нижних частот с крутизной фронта 12 дБ, изображенной на рис. 8.22, анализ Transient Analysis + Parametric Sweep, чтобы исследовать ее переходную характеристику при различных уровнях импеданса.

Для этого выполните в окне Transient…такую же предварительную установку основного анализа, как на рис. 8.21. В качестве дополнительной переменной выберите параметр k, задав его в соответствии с образцом на рис. 8.27, чтобы уровень полного сопротивления фильтра оставался одинаковым при любых значениях k.

1. Выведите на экран PROBE диаграмму, изображенную на рис. 8.29.

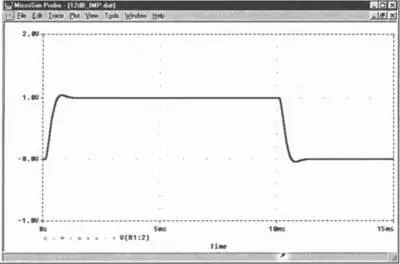
Рис. 8.29. Переходная характеристика фильтра нижних частот с крутизной фронта 12 дБ при различных уровнях импеданса

2. Варьируя значение R, оптимизируйте фильтр таким образом, чтобы добиться оптимальной переходной характеристики для всех уровней импеданса.

Рецепт 1. Провести параметрический анализ

1. Проведите предварительную установку основного анализа. Выберите в качестве изменяемой переменной одну из следующих величин:

• для анализа DC Sweep:

- источник напряжения;

- источник тока;

- модельный параметр;

- глобальный параметр;

- температуру;

(см. рецепты 1-5 в главе 7)

• для анализа AC Sweep:

- частоту;

(см. рецепт 1 в главе 5)

• для анализа переходных процессов:

- время.

(см. рецепт 1 в главе 4).

2. Определите значение, предусмотренное в качестве дополнительной переменной, как параметр в двух местах на чертеже своей схемы:

• дважды щелкните по текущему значению выбранной величины, чтобы открыть окно Set Attribute Value. Присвойте этому параметру имя и заключите его в фигурные скобки (например, замените значение сопротивления 100 Ом именем {R_Tiefpass} — см. рис. 8.8);

• достаньте из библиотеки SPECIAL.slb компонент PARAM и установите его на своем рабочем листе. Дважды щелкните по элементу, чтобы открыть окно его атрибутов. Введите для атрибута Name 1 присвоенное параметру имя, например R_Tiefpass (на этот раз без фигурных скобок). Для атрибута Value 1укажите определенное значение, например 100, которое будет использоваться программой в том случае, если при моделировании данный параметр (Name 1, Value 1)не будет выбран вами в качестве изменяемой переменной, так как вы решите изменять другой параметр (Name 2, Value 2) — см. рис. 8.8.

3. Выведите на экран окно Analysis Setup. Щелкните по кнопке Parametric…, чтобы открыть окно Parametric(см. рис. 8.11).

4. Выполните в этом окне необходимые настройки (см. рис. 8.11), затем щелкните по кнопке OK.

5. В появившемся окне Analysis Setupустановите флажок как рядом с кнопкой основного анализа (например, DC Sweep…), так и рядом с кнопкой дополнительного анализа (кнопка Parametric…), чтобы выполнялись оба этих анализа.

6. Закройте окно Analysis Setup, щелкнув по кнопке Close.

7. Запустите процесс моделирования.

8. После завершения моделирования выберите в окне Available Sections(см рис. 8.5) необходимые кривые (как правило, для отображения требуются все имеющиеся в наличии кривые, в таком случае можно, ничего не меняя в содержании этого окна, просто щелкнуть по кнопке OK).

9. Откройте список диаграмм (команда Trace→Add), выберите необходимы для отображения величины и выведите их на экран PROBE.

(См. раздел 8.2.)

Этот урок посвящен специальным видам анализов, выполняемых с помощью программы PSPICE. Освоив предлагаемый материал, вы сможете самостоятельно исследовать частотные спектры компонентов схемы, определять, насколько эффективно моделирование, каковы возможные допуски устанавливаемых значений и многое другое.

Программа PSPICE может также проводить анализы Фурье (спектральные анализы) и определять с их помощью частотные спектры заданных сигналов. В следующем разделе мы рассмотрим это на примере двух сигналов: сначала с прямоугольным симметричным переменным напряжением частотой f=1 кГц и затем с выходным напряжением транзисторного усилителя.