Роберт Хайнеманн - Визуальное моделирование электронных схем в PSPICE

На диаграмме отчетливо видно, что фильтр оптимально, то есть наиболее быстро, работает только при одном единственном значении R H, и без выбросов достигает своего конечного состояния. Частотная характеристика фильтра также была оптимальной при одном единственном значении нагрузочного резистора (см. рис. 8.19), а именно для R H=8 Ом. Хочется надеяться, что значение сопротивления 8 Ом также окажется оптимальным и для переходной характеристики (импульсной характеристики).

Шаг 31Увеличьте фрагмент диаграммы, изображённой на рис. 8.25, во фронтальной области импульса и определите значение сопротивления, при котором переходная характеристика фильтра является оптимальной (рис. 8.26).

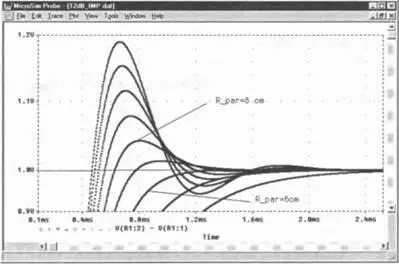
Рис. 8.26. Увеличенный фрагмент диаграммы

Увеличенный фрагмент диаграммы ясно показывает, что переходная характеристика данного фильтра является наиболее оптимальной при подключении к динамику с сопротивлением около 6 Ом.

Шаг 32Увеличьте аналогичным образом другой фрагмент той же диаграммы, на этот раз в области затухания импульса, и убедитесь, что процесс затухания импульса данного фильтра является оптимальным также при значении сопротивления около 6 Ом.

Как выяснилось, частотная характеристика и импульсная характеристика частотных фильтров не оптимизируются одним и тем же значением сопротивления. Таким образом, вы вплотную столкнулись с центральной проблемой, возникающей при проектировании частотных фильтров: как найти компромисс между оптимальным процессом установления и затухания импульса и оптимальным разделением частоты. Частотные фильтры, сконструированные так, что их частотная характеристика оптимизирована за счет характеристики установления и затухания импульса, называют фильтрами с характеристикой Баттерворта. Частотные фильтры, переходная характеристика которых оптимизирована за счет частотной характеристики, называют фильтрами с характеристикой Бесселя.

До сих пор вы называли глобальными параметрами только значения компонентов, то есть сопротивление резисторов, индуктивность катушек и емкость конденсаторов. Однако за понятием «глобальный» кроется гораздо больше. Один и тот же глобальный параметр можно установить в нескольких местах одной схемы и затем изменять его в ходе анализа.

Рассмотрим такой способ установления глобального параметра на примере схемы фильтра нижних частот RLC_MIX1.sch, изображенной на рис. 5.19. При этом исследуем влияние уровня импеданса на характеристику частотного фильтра, то есть выясним, как изменяется частотная характеристика, если R, L и С изменяются так, чтобы активное сопротивление R изменялось с тем же коэффициентом, что реактивные сопротивления X Lи Х С. Для того чтобы увеличить X Lи Х Сна коэффициент k, нужно индуктивность L умножить на коэффициент k, а емкость С разделить на коэффициент k.

Шаг 33Загрузите на экран SCHEMATICS схему RLC_MIX1.sch, подготовьте ее к проведению анализа AC Sweep + Parametric Sweep с параметром k (рис. 8.27) и сохраните измененную схему в папке Projects под именем 12dB_k.sch.

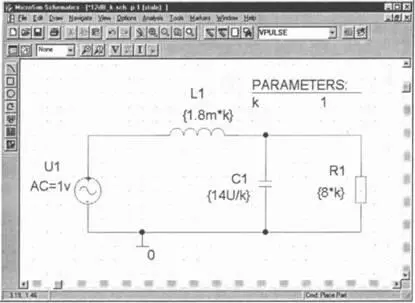
Рис. 8.27. Схема, подготовленная к анализу влияния уровня импеданса на частотную характеристику

Шаг 34Установите источник напряжения на АС=1 В и проведите в окне AC Sweep and Noise Analysisпредварительную установку для основного анализа AC Sweep, в ходе которого будет исследована частотная характеристика фильтра нижних частот в диапазоне от f=10 Гц до f=99 кГц с логарифмическим распределением контрольных точек по 100 точек на каждую декаду.

Шаг 35Откройте окно Parametricи задайте изменение коэффициента k как глобального параметра. При этом варьируйте k от k=0.4 до k=2 с интервалами в 0.2.

Шаг 36Установите в окне Analysis Setupфлажки рядом с кнопками AC Sweep…и Parametric….

Шаг 37Запустите процесс моделирования и выведите на экран PROBE диаграмму, показанную на рис. 8.28.

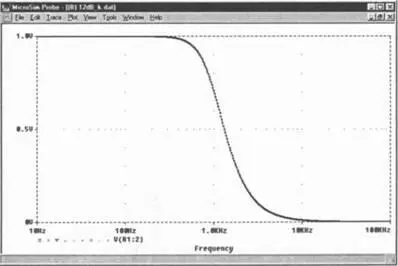
Рис. 8.28. Диаграмма с результатами моделирования схемы фильтра нижних частот при различных уровнях импеданса