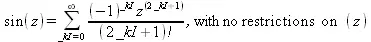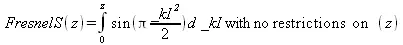Владимир Дьяконов - Maple 9.5/10 в математике, физике и образовании

Рис. 3.14. Примеры работы со специальными математическими функциями

На рис. 3.14 показаны примеры разложения специальных функций в ряды и применения функции convert для их преобразования. Любопытно отметить, что в двух первых примерах рис. 3.14 вывод оказался иным, чем в предшествующих версиях Maple. Да и в них вывод для этих примеров отличался. Это говорит о непрерывной работе разработчиков над алгоритмами символьных вычислений и необходимости переработки примеров при переходе от одной версии Maple к другой.

Много информации о поведении специальных функций дает построение их графиков. На рис. 3.15 показано построение семейства графиков функций Бесселя BesselJ разного порядка и гамма-функции. Эти функции относятся к числу наиболее известных. Если читателя интересуют те или иные специальные функции, следует прежде всего построить и изучить их графики.

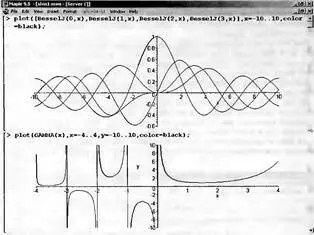
Рис. 3.15. Графики функций Бесселя и гамма-функции

Математикам, серьезно работающим с функциями, большую помощь может оказать имеющийся в составе Maple 9.5 консультант по функциям, вводимый командой:

FunctionAdvisor()

FunctionAdvisor(topics, quiet)

FunctionAdvisor(Topic, function, quiet)

Здесь: topics — строковый параметр, задающий вывод тематической информации, quiet — строковый параметр, указывающий на вывод вычислительных данных, Topic — задание темы и function — задание имени функции или класса функций.

Команда FunctionAdvisor() выводит правила применения консультанта по функциям (файл funcadv):

> FunctionAdvisor(); The usage is as follows:

> FunctionAdvisor( topic, function, ... );

where 'topic' indicates the subject on which advice is required, 'function' is the name of a Maple function, and '...' represents possible additional input depending on the 'topic' chosen. To list the possible topics:

> FunctionAdvisor( topics ); A short form usage,

> FunctionAdvisor(function);

with just the name of the function is also available and displays a summary of information about the function.

Следующие примеры показывают вывод определений функций Бесселя:

> FunctionAdvisor(describe, Bessel);

BesselI = Modified Bessel function of the first kind,

BesselJ = Bessel function of the first kind,

BesselK = Modified Bessel function of the second kind,

BesselY = Bessel function of the second kind

> FunctionAdvisor(describe, BesselJ);

BesselJ = Bessel function of the first kind

В следующем примере выводится информация о представлении функции синуса в виде ряда, представленного суммой его членов:

> FunctionAdvisor(sum_form, sin);

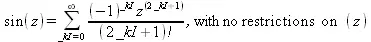
Еще один пример показывает вывод интегрального представления синусного интеграла Френеля:

> FunctionAdvisor(integral form, FresnelS);

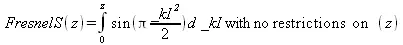
Представленные примеры дают представление лишь о малой части возможностей консультанта по функциям. С этим мощным средством получения информации о функциях можно дополнительно познакомиться по справке о нем, содержащей множество интересных примеров применения консультанта по функциям.

Функции комбинаторики достаточно известны из обычного курса математики. Но они применяются сравнительно редко. Поэтому они не включены в состав ядра системы, но имеются в пакете расширения combinat. При вызове пакета

> with(combinat);

выводится список имен его функций. Ввиду важности функций комбинаторики для некоторых специальных вычислений приведем их полные определения:

• Chi(x) — гиперболический косинусный интеграл;

• bell(n) — возвращает числа из решения уравнения ехр(ехр(х)-1)= sum(bell(n)/n!*x^n, n=0..infinity), причем для вычислений используется рекуррентное соотношение bell(n+1) = (bell(n)+1)^n;

• binomial(n, r) — возвращает биноминальные коэффициенты, причем, если n и r — целые числа, удовлетворяющие условию 0<=r<=n, то функция возвращает C(n,r)=n!/(r!(n-r)!), а в общем случае C(n, r) = limit(GAMMA(N+1)/ GAMMA(R+1)/GAMMA(N-R+1),R=r,N=n).

• composition(n, k) — возвращает списки композиций для целых неотрицательных n и k;

• fibonacci(n) — возвращает числа Фибоначчи, вычисляемые по рекуррентной формуле F(n) = F(n–1)+F(n –2), где F(0) = 0 и F(1)=1;