Владимир Дьяконов - Maple 9.5/10 в математике, физике и образовании

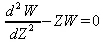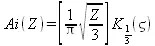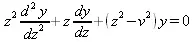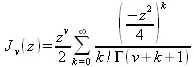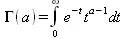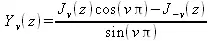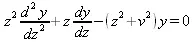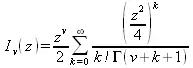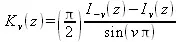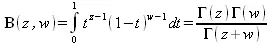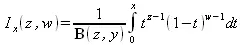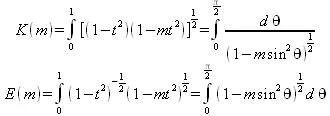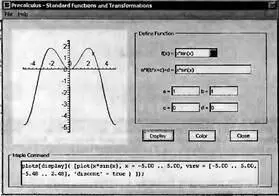
Рис. 3.12. Maplet-окно для изучения функций и построения их графиков

В окне в разделе определения функций Define Function имеется список элементарных функций, графики которых можно просматривать. Однако, возможно построение и графиков простых функций более сложного вида, например x*sin(x) вместо sin(x) — это и иллюстрирует график, представленный на рис. 3.12. Maplet-окно генерирует команду на Maple-языке, которая строит график заданной функции.

Специальные математические функции являются решениями дифференциальных уравнений, которые невозможно представить через элементарные функции. Через такие функции нередко представляются и многие интегралы. Наиболее мощные из СКМ, например Maple, широко используют специальные математические функции в ходе символьных преобразований. Рассмотрим наиболее важные специальные математические функции.

Функция Эйри формирует пару линейно независимых решений дифференциального уравнения вида:

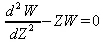
Связь между функцией Эйри и модифицированной функцией Бесселя выражается формулой:

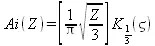
где

Дифференциальное уравнение вида

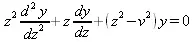
где v — неотрицательная константа, называется уравнением Бесселя, а его решения известны как функция Бесселя. J(z)и J _ (z)формируют фундаментальное множество решений уравнения Бесселя для неотрицательных значений (так называемые функции Бесселя первого рода):

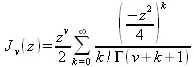
где для гамма-функции используется следующее представление:

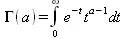
Второе решение уравнения Бесселя, линейно независимое от J(z), определяется как

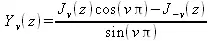
и задает функции Бесселя второго рода Y(z).

Функции Бесселя третьего рода (функции Ханкеля) и функция Бесселя связаны следующим выражением:

H (1) v ( z ) = J v ( z ) + iY v (z),

H (2) v ( z ) = J v ( z ) - iY v (z).

Дифференциальное уравнение вида

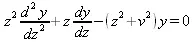
где v — неотрицательная константа — называется модифицированным уравнением Бесселя, и его решения известны как модифицированные функции Бесселя I(z)и I _ (z). K(z)— второе решение модифицированного уравнения Бесселя, линейно независимое от I(z). I(z)и K(z)определяются как:

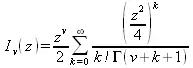
и

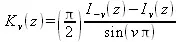
Бета-функция определяется как:

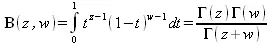
где Г(z) — гамма-функция. Неполная бета-функция определяется интегральным выражением:

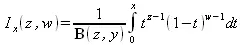
Эллиптические функции Якоби определяются интегралом:

В некоторых случаях при определении эллиптических функций используются модули k вместо параметра m. Они связаны выражением:

k² = m = sin² α.

Полные эллиптические интегралы первого и второго рода определяются следующим образом:

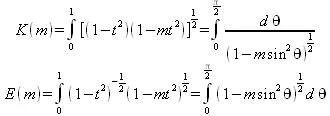
Функция ошибки (интеграл вероятности) определяется следующим образом: