Владимир Дьяконов - Maple 9.5/10 в математике, физике и образовании

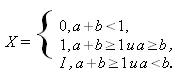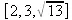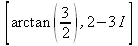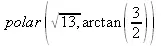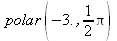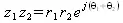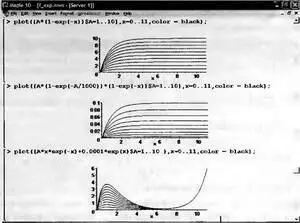
Рис. 3.10. Конец документа с началом на рис. 3.7

Последняя зависимость неплохо подходит для приближения N-образной вольт-амперной характеристики туннельного диода. Это довольно старый, но хорошо известный прибор, который применяется в усилителях и генераторах высокочастотных и сверхвысокочастотных колебаний.

В алгоритме вычисления ряда функций заложено сравнение результата с некоторым опорным значением. К таким функциям с элементами сравнения относятся: abs — абсолютное значение числа; ceil — наименьшее целое, большее или равное аргументу; floor — наибольшее целое, меньшее или равное аргументу; frac — дробная часть числа; trunc — целое, округленное в направлении нуля; round — округленное значение числа; signum(х) — знак х (-1 при х <0, 0 при х =0 и +1 при х >0).

Для комплексного аргумента х эти функции определяются следующим образом:

• trunc(x) = trunc(Re(x)) + rtrunc(Im(x));

• round(x) = round(Re(x)) + I*round(Im(x));

• frac(x) = frac(Re(x)) + I*frac(Im(x)).

Для введения определения значения floor(x) от комплексного аргумента прежде всего запишем а=Re(x)-floor(Re(x)) и b=Im(x)-floor(Im(x)). Тогда floor(x)=floor(Re(x))+I*floor(Im(x))+X, где

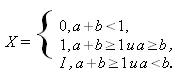
Наконец, функция ceil для комплексного аргумента определяется следующим образом:

ceil(x) = -floor(-х)

Примеры вычисления выражений с данными функциями представлены ниже (файл calcfun):

> [ceil(Pi), trunc(Pi), floor(Pi), frac(Pi), round(Pi)];

> frac(evalf(Pi));

> [ceil(-Pi),trunc(-Pi),floor(-Pi),round(-Pi)];

> trunc(2.6+3.4*I);

> [signum(-Pi),signum(0),signum(Pi)];

Хотя функции этой группы достаточно просты, их нельзя относить к числу элементарных функций. Нередко их применение исключает возможность проведения символьных преобразований или дает их существенное усложнение.

Для комплексных чисел и данных, помимо упомянутых в предшествующем разделе, определен следующий ряд базовых функций: argument — аргумент комплексного числа; conjugate — комплексно-сопряженное число; Im — мнимая часть комплексного числа; Re — действительная часть комплексного числа; polar — полярное представление комплексного числа (библиотечная функция). Примеры вычисления для этих функций (файл calcfun):

> z:=2+3*I;

> [Re(z),Im(z),abs(z)];

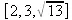
> [argument(z),conjugate(z)];

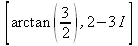
> readlib(polar);

> polar(z);

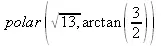
> polar(-3.,Pi/2);

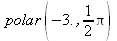
В некоторых случаях полезна визуализация операций с комплексными числами. Для этого удобен пакет расширения plots, который позволяет представлять комплексные числа в виде стрелок на комплексной плоскости. Например, для иллюстрации операции умножения двух комплексных чисел

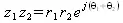
можно использовать следующие графические построения (файл complpot):

> with(plottools):

l1 := arrow([0,0], [1,2], .1, .3, .1, color=green):

l1a := arc([0,0],1.5,0..arctan(2),color=green):

> l2 := arrow([0,0], [1,-8], .1, .3, .1, color=green):

l2a := arc([0,0],.75,0..arctan(.8),color=green):

> l3 := arrow([0,0], [-.6,2.8], .1, .3, .1, color=black):

l3a := arc([0,0],2.5,0..arctan(2.8,-.6),color=black):

> plots[display](l1,l2,l3,l1a,l2a,l3a, axes=normal,view=[-3..3,0..3],scaling=constrained);

Они создают график (рис. 3.11) наглядно иллюстрирующий операцию перемножения двух комплексных чисел, представленных своими радиус-векторами.

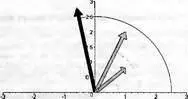
Рис. 3.11. Иллюстрация перемножения двух комплексных чисел

При изучении графиков элементарных функций вне особенностей системы Maple полезно Maplet-приложение, окно которого представлено на рис. 3.12. Открывается это окно исполнением команды Tools→Precalcus→Standard Functions… при работе в стандартном интерфейсе Maple 9.5.