Владимир Дьяконов - Maple 9.5/10 в математике, физике и образовании

> [sin(1), sin(1.)];

> sin(x)^2+cos(x)^2;

> simplify(%);

> simplify(tan(x)*cos(x));

> sec(2+3*1);

> sec(2.+3*I);

> cot(I);

> csc(I);

Многие свойства тригонометрических функций можно оценить, рассматривая их графики. Для построения таких графиков средствами Maple можно использовать функцию plot. Примеры построения графиков тригонометрических функций даны в файле tfris.

Фундаментальная роль функций синуса и косинуса проявляется в решении задач спектрального анализа и синтеза. В Maple они реализуются с помощью функций прямого и обратного преобразований Фурье [39, 43]. Однако, смысл гармонического синтеза проще всего понять, просто суммируя синусоидальные функции с кратной частотой — гармоники. При этом характер результирующего колебания зависит от того, какие гармоники берутся (все, только четные или только нечетные), а также от того, по какому закону меняется амплитуда колебаний и их фаза в зависимости от номера гармоники. Покажем это на паре примеров.

На рис. 3.2 показан пример гармонического синтеза двух периодов пилообразного колебания (сигнала) при суммировании 3, 10 и 60 гармоник. Отчетливо видно, что по мере увеличения числа гармоник форма колебаний действительно приближается к треугольной. В условиях резкого ограничения числа гармоник в местах предполагаемого разрыва колебаний наблюдаются характерные колебания — эффект Гиббса.

Рис. 3.2. Гармонический синтез треугольных колебаний по 3, 10 и 60 гармоникам

Колебания описанной формы получаются за счет синтеза всех гармоник, причем амплитуда гармоник равна 1/k, где k — номер гармоники.

А теперь рассмотрим синтез симметричных прямоугольных колебаний, получивших название — меандр. Для синтеза меандра надо использовать только нечетные гармоники, т. е. с номерами n=1, 3, 5, … Проще всего получить нечетные числа, используя вместо параметра n значение 2n–1. Тогда для получения 3, 9 и 59 нечетных гармоник надо будет использовать значения n до 2, 5 и 30. Рис. 3.3 иллюстрирует синтез меандра.

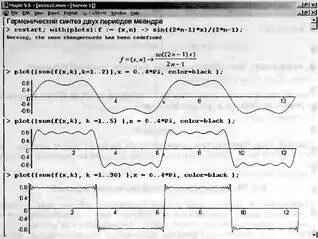
Рис. 3.3. Гармонический синтез меандра при n = 2, 5 и 30

Читатель, интересующийся вопросами гармонического синтеза сигналов может опробовать в нем свои силы и синтезировать колебания и сигналы других форм. Поскольку при синтезе сигнал получается в виде частотных составляющих (гармоник), то для преобразования такого сигнала можно использовать частотные фильтры.

К обратным тригонометрическим функциям относятся: arcsin — арксинус; arccos — арккосинус; arctan — арктангенс; arcsec — арксеканс; arccsc — арккосеканс; arccot — арккотангенс. Примеры вычислений (файл calcfun):

> arcsin(.2);

> arcsin(2.);

> evalc(arcsin(5));

> arccos(1/2);

> arctan(1);

> arccot(0);

К этому классу функций принадлежит еще одна полезная функция:

arctan(y,x) = argument(х+I*у)

Она возвращает угол радиус-вектора в интервале от -Pi до Pi при координатах конца радиус-вектора х и у (см. пример ниже):

> arctan(2., 3);

Графики ряда обратных тригонометрических функций строит документ, имеющийся в файле tfris. Следует отметить, что эти функции не являются периодическими.

Гиперболические функции представлены следующим набором: sinh — гиперболический синус; cosh — гиперболический косинус; tanh — гиперболический тангенс; sech — гиперболический секанс; csch — гиперболический косеканс; coth — гиперболический котангенс. Примеры применения гиперболических функций представлены ниже (файл calcfun):

> [sinh(1.), cosh(1.), tanh(1.)];

> [sech(1.), csch(1.), coth(1.)];

На рис. 3.4 сверху представлены графики гиперболического синуса, косинуса и тангенса. По ним можно судить о поведении этих функций.