Владимир Дьяконов - Maple 9.5/10 в математике, физике и образовании

Функции обычно подразделяются на четыре типа:

• встроенные в ядро системы предопределенные функции или внутренние функции;

• функции пользователя;

• библиотечные функции, вызываемые из пакетов или библиотек расширения системы, например sin(x) или ln(x);

• функции, заданные в виде программного модуля.

Кроме того, функции могут классифицироваться по характеру производимых ими преобразований входных параметров. Они делятся на алгебраические, тригонометрические, обратные тригонометрические, гиперболические, обратные гиперболические, специальные и так далее.

В математических системах Maple функции могут применяться со специальными директивами и опциями. Они могут задаваться как дополнительный параметр функции.

Математические выражения это сложные (комбинированные) объекты, которые состоят из операторов, операндов и функций со списками их параметров. Например, в выражении (2+3)*sin(x) скобки ( ) и знаки + и * являются операторами, константы 2 и 3 — операндами, sin(x) — встроенной функцией, а х — входным параметром функции. Для оператора умножения выражение (2+3) и функция sin(x), т.е. по существу тоже выражение, являются операторами. Приоритет функций более высокий, чем у операторов.

В системах для численных расчетов математические выражения применяются в естественном виде и в разборе их структуры нет особой необходимости. Исключение составляет разве что анализ скобок, меняющих приоритет выполнения операций в выражениях.

Иное дела системы символьной математики. У них в ходе вычислений выражения эволюционируют , то есть видоизменяются по мере выполнения расчетов. Это может приводить к весьма неожиданным последствиям, например, когда сложнейшее выражение упрощается к 0 или 1, а внешне совсем не страшное выражение разворачивается так, что не помещается в десятке страниц экрана. Набор средств по разбору структуры и преобразованиям математических выражений в таких системах настолько велик, что всерьез разобраться с ними под силу математику-аналитику или достаточно опытному пользователю. Поэтому мы оставим рассмотрение функций анализа выражений на потом — оно будет дано при описании средств символьной математики.

Maple имеет полный набор элементарных математических функций [38–41]. Все они, кроме арктангенса двух аргументов, имеют один аргумент х, например sin(x). Он может быть целым, рациональным, дробно-рациональным, вещественным или комплексным числом. В ответ на обращение к ним элементарные функции возвращают соответствующее значение. Поэтому они могут быть включены в математические выражения. Все описанные здесь функции называются встроенными, поскольку они реализованы в ядре системы.

Как правило, если аргументом функции является фундаментальная константа, целое или рациональное число, то функция выводится с таким аргументом без получения результата в форме действительного числа с плавающей точкой. Например (файл calcfun):

> sin(Pi);

> sin(1);

> exp(1);

> ln(2);

> ln(Pi);

> arcsin(1/2);

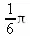
> arcsin(1/3);

Нетрудно заметить, что есть и исключения из этого правила — например, на экране монитора ехр(1) будет выведено как константа е, а значение функции arcsin(1/2) все же вычислено и результат получен как 1/6 от константы Pi. Вообще говоря, если результат выражается через фундаментальную математическую константу, то он будет вычислен и представлен ею. В противном случае функция с целочисленным и рациональным аргументом или с константой просто повторяется в строке вывода в установленном для этой строки формате.

Для получения подробной информации о некоторой произвольной функции достаточно задать команду

> ?

Например, команда

> ? sin

открывает окно справки по тригонометрическим функциям, включая функцию синуса.

Ввиду общеизвестности элементарных функций мы не будем обсуждать ни их свойства, ни допустимые для них пределы изменения аргумента. Эти вопросы отражаются в любом учебнике по элементарной математике.

Ниже представлены наиболее распространенные целочисленные функции Maple, используемые в теории чисел: