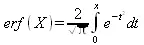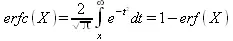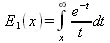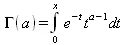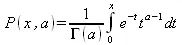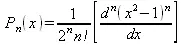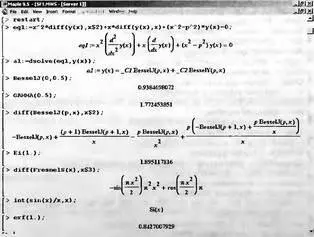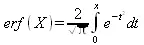
erf(X)— возвращает значение функции ошибки для каждого элемента вещественного массива X.
Остаточная функция ошибки задается соотношением:
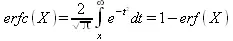
Встречается и масштабированная остаточная функция ошибки. Эта функция определяется так:
eifcx(x) = е x²erfc(x)
Интегральная показательная функция определяется следующим образом:
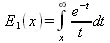
Гамма-функция определяется выражением:
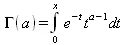
Неполная гамма-функция определяется как:
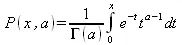
Перейдем к функциям, представляющим ортогональные полиномы. Функция Лежандра определяется следующим образом:

где Р n (х) — полином Лежандра степени n, определяется так:
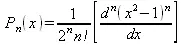
3.3.2. Специальные математические функции системы Maple 9.5
Maple 9.5 имеет практически полный набор специальных математических функций:
• AiryAi (Bi) — функции Эйри;
• AngerJ — функция Ангера;
• bernoulli — числа и полиномы Бернулли;
• Bessell (J, K, Y) — функции Бесселя разного рода;
• Beta — бета-функция;
• binomial — биноминальные коэффициенты;
• Chi — интегральный гиперболический косинус;
• Сi — интегральный косинус;
• csgn — комплексная сигнум-функция;
• dilog — дилогарифм;
• Dirac — дельта-функция Дирака;
• Ei — экспоненциальный интеграл;
• EllipticCE (CK, CPi, Е, F, K, Modulus, Nome, Pi) — эллиптические интегралы;
• erf — функция ошибок;
• erfc — дополнительная функция ошибок;
• euler — числа и полиномы Эйлера;
• FresneIC (f, g, S) — интегралы Френеля;
• GAMMA — гамма-функция;
• GaussAGM — арифметико-геометрическое среднее Гаусса;
• HankelH1 (Н2) — функции Ганкеля;
• harmonic — частичная сумма серии гармоник;
• Heaviside — функция Хевисайда;
• JacobiAM (CN, CD, CS, DN, DC, DS, NC, ND, NS, SC, SD, SN) — эллиптические функции Якоби;
• JacobiTheta1 (2, 3, 4) — дзета-функции Якоби;
• JacobiZeta — зет-функция Якоби;
• KelvinBer (Bei, Her, Hei, Ker, Kei) — функции Кельвина;
• Li — логарифмический интеграл;
• InGAMMA — логарифмическая гамма-функция;
• MeijerG — G-функция Мейджера;
• pochhammer — символ Похгамера;
• polylog — полилогарифмическая функция;
• Psi — дигамма-функция;
• Shi — интегральный гиперболический синус;
• Si — интегральный синус;
• Ssi — синусный интеграл смещения;
• StruveH (L) — функции Струве;
• surd — неглавная корневая функция;
• LambertW — W-функция Ламберта;
• WeberE — Е-функция Вебера;
• WeierstrassP — Р-функция Вейерштрасса;
• WeierstrassPPrime — производная Р-функции Вейерштрасса;
• WeierstrassZeta — зета-функция Вейерштрасса;
• WeierstrassSigma — сигма-функция Вейерштрасса;
• Zeta — зета-функция Римана и Гурвица.
Ввиду большого числа специальных функций и наличия множества примеров их вычисления в справочной системе Maple 9.5, ограничимся несколькими примерами вычисления наиболее распространенных специальных функций. По их подобию читатель может опробовать в работе и другие специальные функции.
На рис. 3.13 даны примеры применения ряда специальных функций. Обратите особое внимание на первый пример. Он показывает, как средствами системы Maple задается определение функций Бесселя. Показано, что функции Бесселя являются решениями заданного на рис. 3.13 дифференциального уравнения второго порядка. Система Maple 9.5/10 способна вычислять производные и интегралы от специальных функций.
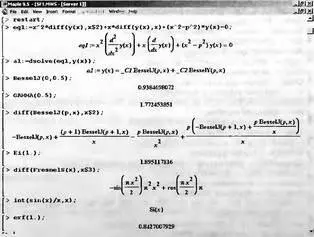
Рис. 3.13. Примеры применения специальных функций
Еще несколько примеров работы со специальными функциями представлено на рис. 3.14. Как видно из приведенных примеров, на экране монитора можно получить математически ориентированное представление специальных функций, обычно более предпочтительное, чем представление на Maple-языке или в текстовом формате. Записи функций при этом выглядят как в обычной математической литературе.
Читать дальше
Конец ознакомительного отрывка
Купить книгу