Владимир Дьяконов - Maple 9.5/10 в математике, физике и образовании

Более обширные возможности анимации двумерных графиков обеспечивает функция animate:

animate(F, х, t)

animate(F, x, t, o)

В ней параметр x задает пределы изменения переменной х, а параметр t — пределы изменения дополнительной переменной t. Суть анимации при использовании данной функции заключается в построении серии кадров (как в мультфильме), причем каждый кадр связан со значением изменяемой во времени переменной t. Если надо явно задать число кадров анимации N, то в качестве о следует использовать frame=N.

Рисунок 8.38 показывает применение функции animate.

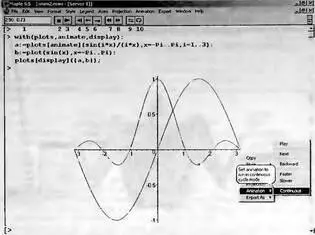
Рис. 8.38. Анимация функции sin(i*x)/(i*x) на фоне неподвижной синусоиды

В документе рис. 8.38 строятся две функции — не создающая анимации функция sin(x) и создающая анимацию функция sin (i*x)/(i*x), причем в качестве переменной t задана переменная i. Именно ее изменение и создает эффект анимации. Проигрыватель анимационных клипов и меню, описанные выше, могут использоваться для управления и этим видом анимации. Обратите внимание на вызов графических функций в этом примере командой with и на синтаксис записи этих функций.

К сожалению, картинки в книгах всегда неподвижны и воспроизвести эффект анимации невозможно. Можно лишь представить несколько текущих кадров анимации. Представленная на рис. 8.38 картина соответствует последнему кадру анимации.

Анимация графиков может найти самое широкое применение при создании учебных материалов. С ее помощью можно акцентировать внимание на отдельных параметрах графиков и образующих их функций и наглядно иллюстрировать характер их изменений.

Аналогичным образом может осуществляться и анимация трехмерных фигур. Для этого используется функция animate3d:

animate3d(F,х,у,t,o)

Здесь F — описание функции (или функций); х, у и t — диапазоны изменения переменных х, у и t. Для задания числа кадров N надо использовать необязательный параметр о в виде frame=N. Примеры применения этой функции мы рассмотрим позже.

На рис. 8.39 показано построение графика с анимацией. После задания функции, график которой строится, необходимо выделить график и запустить проигрыватель, как это описывалось для анимации двумерных графиков.

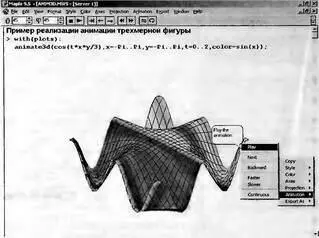
Рис. 8.39. Подготовка трехмерного анимационного графика

На рис. 8.39 показано также контекстное меню поля выделенного графика. Нетрудно заметить, что с помощью этого меню (и содержащихся в нем подменю) можно получить доступ к параметрам трехмерной графики и выполнить необходимые операции форматирования, такие как включение цветовой окраски, выбор ориентации фигуры и т.д.

Назначение параметров, как и средств управления проигрывателем анимационных клипов, было описано выше.

Еще один путь получения анимационных рисунков — создание ряда графических объектов p1, p2, p3 и т.д. и их последовательный вывод с помощью функций display или display3d:

display(p1,p2,р3,..nsequence=true)

display3d(p1,p2,p3...,insequence=true)

Здесь основным моментом является применение параметра insequence=true. Именно он обеспечивает вывод одного за другим серии графических объектов р1, р2, p3 и т.д. При этом объекты появляются по одному, и каждый предшествующий объект стирается перед появлением нового объекта. Этот метод анимации мы рассмотрим чуть позже.

Инструментальный пакет графики plottools служит для создания графических примитивов, строящих элементарные геометрические объекты на плоскости и в пространстве: отрезки прямых и дуг, окружности, конусы, кубики и т.д. Его применение позволяет разнообразить графические построения и строить множество графиков специального назначения. В пакет входят следующие графические примитивы:

arc arrow circle cone cuboid

curve cutin cutout cylinder disk

dodecahedron ellipse ellipticArc hemisphere hexahedron

hyperbola icosahedron line octahedron pieslice

point polygon rectangle semitorus sphere

tetrahedron torus