Владимир Дьяконов - Maple 9.5/10 в математике, физике и образовании

Еще один распространенный способ представления трехмерных поверхностей — графики полей векторов. Они часто применяются для отображения полей, например электрических зарядов. Особенность таких графиков в том, что для их построения используют стрелки, направление которых соответствует направлению изменения градиента поля, а длина — значению градиента. Так что термин «поле векторов» надо понимать в смысле, что поле графика заполнено векторами.

Для построения таких графиков в двумерной системе координат используется функция fieldplot:

fieldplot(f, r1, r2)

fieldplot(f, r1, r2, ...)

где f — вектор или множество векторов, задающих построение; r1 и r2 — пределы.

На рис. 8.26 в нижней части документа показан вид одного из таких графиков. Следует отметить, что для получения достаточного числа отчетливо видных стрелок надо поработать с форматированием графиков. Иначе графики этого типа могут оказаться не очень представительными. Так, слишком короткие стрелки превращаются в черточки и даже точки, не имеющие острия, что лишает графики наглядности.

Трехмерные поверхности также могут задаваться уравнениями неявного вида. В этом случае для построения их графиков используется функция implicitplot3d:

implicitplot3d(expr1,х=а..b,y=c..d,z=p..q,)

implicitplot3d(f,a..b,c..d,p..q, )

На рис. 8.27 показаны два примера построения любопытных объемных фигур с помощью функции implicitplot3d.

Рис. 8.27. Примеры применения функции implicitplot3d

Эти примеры, взятые из справки, хорошо иллюстрируют технику применения функции implicitplot3d. С ее помощью можно строить весьма своеобразные фигуры, что, впрочем, видно и из приведенных примеров. Для наглядности фигур рис. 8.40 они несколько развернуты в пространстве с помощью мыши.

В пакете plots имеется множество функций для построения графиков в различных системах координат Объем книги не позволяет воспроизвести примеры всех видов таких графиков, ибо их многие сотни. Да это и не надо — во встроенных в справочную систему примерах можно найти все нужные сведения. Так что ограничимся лишь парой примеров применения функции tubeplot(C, options), позволяющей строить весьма наглядные фигуры в пространстве, напоминающие трубы или иные объекты, образованные фигурами вращения.

На рис. 8.28 показана одна из таких фигур. Она поразительно напоминает раковину улитки. Функциональная окраска достигнута доработкой графика с помощью панели форматирования — она, как и контекстное меню правой клавиши мыши, показана на рис. 8.28.

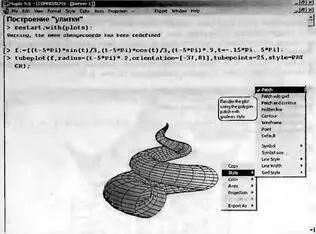
Рис. 8.28. Построение графика — «раковина улитки»

Эта функция может использоваться и для построения ряда трубчатых объектов в пространстве. При этом автоматически задается алгоритм удаления невидимых линий даже для достаточно сложных фигур. Это наглядно иллюстрирует пример на рис. 8.29, показывающий фигуру «цепи». Не правда ли, реалистичность этой фигуры поражает воображение?

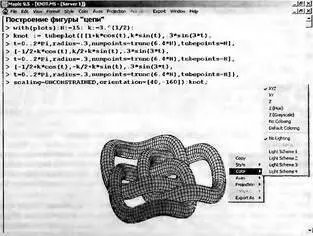
Рис. 8.29. Фигура «цепи», построенная с применением функции tubeplot

Можно долго размышлять о том, как те или иные математические закономерности описывают предметы реального мира, положенные в основу тех или иных геометрических объектов или, возможно, о гениальности людей, сумевших найти такие закономерности для многих из таких объектов. В наше время Maple открывает огромные возможности для таких людей.

Наглядность ряда графиков можно существенно увеличить, строя их в трехмерном представлении. Например, для такого построения графиков полей из векторов можно использовать графическую функцию fieldplot3d. В отличие от функции fieldplot она строит стрелки как бы в трехмерном пространстве (рис. 8.30). Возможности смены осей о оформления «ящика» графика иллюстрирует контекстное меню правой клавиши мыши, показанное на рис. 8.30.