Владимир Дьяконов - Maple 9.5/10 в математике, физике и образовании

Хорошим примером 3D-анимации является документ, показанный на рис. 8.51. Представленная на нем процедура springPlot имитирует поведение упругой системы, первоначально сжатой, а затем выстреливающей шар, установленный на ее верхней пластине. Упругая система состоит из неподвижного основания, на котором расположена упругая масса (например, из пористой резины), и верхней пластины.

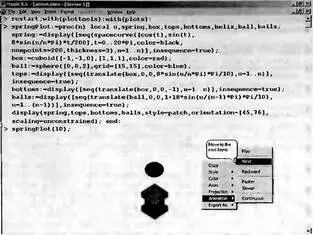
Рис. 8.51. Имитация отстрела шара сжатой упругой системой

Управление анимацией, реализованной средствами пакета plottools, подобно уже описанному ранее. Последний пример также прекрасно иллюстрирует возможности применения Maple 9.5 при математическом моделировании различных явлений, устройств и систем.

Обычно если в строке ввода задается построение нескольких графиков, то в строке вывода все они располагаются по вертикали. Это не всегда удобно, например, при снятии копий экрана с рядом графиков, поскольку экран монитора вытянут по горизонтали, а не по вертикали. Однако при применении функций plots и display можно разместить ряд двумерных графиков в строке вывода по горизонтали. Это демонстрирует пример, показанный на рис. 8.52.

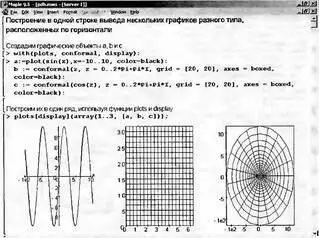
Рис. 8.52. Пример расположения трех графиков в строке вывода по горизонтали

Пример достаточно прост и нагляден, так что читатель может пользоваться данной возможностью всегда, когда ему это нужно.

В пакете plots имеется функция для конформные отображений:

conformal(F, r1, r2, о)

где F — комплексная процедура или выражение; r1, r2 — области, задаваемые в виде а..b или name=a..b; о — управляющие параметры. Таким образом, для построения нужного графика достаточно задать нужное выражение и области изменения r1 и r2. Пример построения конформных изображений для трех выражений дан на рис. 8.53.

Рис. 8.53. Конформное отображение на комплексной плоскости графиков трех зависимостей

Средства конформного отображения в Maple 9.5/10, к сожалению, остаются рудиментарными и вряд ли достаточными для специалистов в этой области математики.

Некоторые виды математической графики имеют определенную художественную ценность и фигурируют в символике различных стран и общественных организаций. Остановимся на нескольких таких примерах применительно к графике в полярной системе координат. Представим фигуры, образованные множеством линий на плоскости.

Рис. 8.54 демонстрирует две из таких фигур. Первая это семейство из 10 кардиоид разного размера, построенных функцией polarplot. Параметр scalling=constrained обеспечивает правильное отображение фигур — каждая кардиоида вписывается в огибающую ее невидимую окружность. Размер кардиоид задается значением параметра а.

Рис. 8.54. Семейство кардиоид на одном графике и крест из пяти фигур на комплексной плоскости

Вторая фигура представляет собой пять фигур, построенных функций complexplot, дающей построение графиков функций комплексной переменной на комплексной плоскости. В данном случае фигуры образуют крест.

По образу и подобию приведенных фигур читатель может опробовать свои силы в создании новых красочных фигур в полярной системе координат. Некоторые из них поразительно напоминают снежинки, картинки в калейдоскопе и изображения морских звезд. Если убрать параметр color=black, введенный ради черно-белой печати картинок в книге, то можно усилить красочность фигур за счет их разноцветной окраски.

Импликативные функции нередко имеют графики весьма любопытного вида. Ограничимся парой примеров построения таких графиков, представленных на рис. 8.55. Эти фигуры напоминают контурные графики функции двух переменных.