Владимир Дьяконов - Maple 9.5/10 в математике, физике и образовании

Жесткие системы дифференциальных уравнений, часто описывают кинетику химических процессов, например, растворение веществ в растворах или смешивание газов.

На рис. 7.24 показано решение жесткой системы из трех дифференциальных уравнений, описывающих один из типовых химических процессов — какой именно в данном случае не важно.

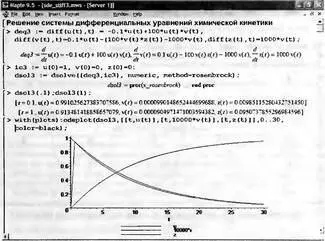
Рис. 7.24. Решение жесткой системы дифференциальных уравнений, описывающей кинетику химического процесса

Классическим примером нелинейного дифференциального уравнения второго порядка, относящегося к жесткому типу по большом значении некоторого параметра mu, относится уравнение Ван-Дер Поля. Важность этого уравнения заключается в том, что к нему довольно просто сводятся дифференциальные уравнения, описывающие динамику развития колебаний в различных колебательных системах, например, автогенераторах на электронных лампах, полевых и биполярных транзисторах.

Пример задания и решения дифференциального уравнения Ван-Дер Поля при сравнительно малом mu=1 (и при выборе метода решения по умолчанию) представлен на рис. 7.25. Нетрудно заметить, что выбор Maple пал на метод rkf45 и что этот метод не очень удачен даже для этого метода с mu=1. Хотя общая форма колебаний (близкая к синусоидальной, но все же заметно искаженная) в интервале t от 0 до 20 просматривается, уже в данном случае видна нестабильность колебаний. При увеличен максимального значения t до 100 и более, нестабильность колебаний становится весьма заметна (проверьте это сами).

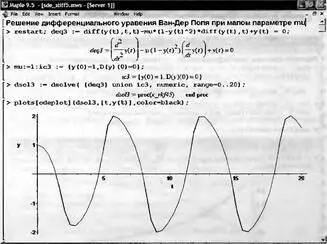
Рис. 7.25 Задание и решение дифференциального уравнения Ван-Дер Поля при сравнительно малом mu=1

Задание и решение дифференциального уравнения Ван-Дер Поля при большом mu=2000 (рис. 7.26) демонстрирует существенное изменение формы временной зависимости колебаний и их параметров. Теперь отчетливо виден разрывный характер колебаний, типичный для релаксационных колебаний. Моделирование колебаний в этом случае методом rkf45 уже невозможно и потому для решения задана опция stiff=true. При этом Maple взял за основу метод Розенброка. Он обеспечивает более качественное моделирование в системе Ван-Дер Поля.

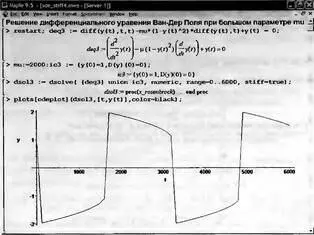
Рис. 7.26. Задание и решение дифференциального уравнения Ван-Дер Поля при большом mu=2000

Дополнительные примеры на решение жестких систем дифференциальных уравнений можно найти в разделах справки по решению таких уравнений.

В решении ряда математических задач нужно найти решение дифференциального уравнения с двумя краевыми условиями. Например, в физике это задача стрельбы по летящей цели. Обычно такая задача решается методом пристрелки, при котором методом проб с итерационным уточнением рассчитывается ряд вариантов решения и выбирается тот, у которого соблюдается начальное условие в начале решения и начальное условие в конце решения с заданной (в частности по умолчанию) погрешностью.

Для такого решения используется функция dsolve в следующем виде:

dsolve(odesys, numeric, vars, options)

Здесь:

• odesys — множество или список обыкновенных дифференциальных уравнений и двойных граничных условии;

• numeric — опция, задающая решение в численном виде;

• vars — опционально заданный параметр, задающий имя переменной в odesys;

• options — опционально заданные равенства (в форме keyword=value), определяющие краевые условия.

Пример решения дифференциального уравнения второго порядка с двумя граничными условиями представлен на рис. 7.27. Отчетливо видно, что найденная зависимость точно удовлетворяет краевым условиям.

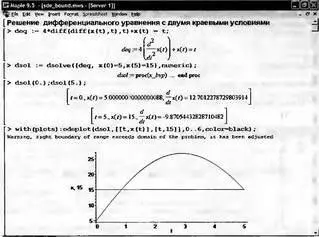
Рис. 7.27. Пример решения дифференциального уравнения второго порядка с двумя граничными условиями