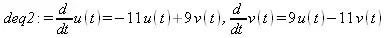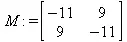Владимир Дьяконов - Maple 9.5/10 в математике, физике и образовании

• действительные части всех собственных значений матрицы А отрицательны, т. е. Re(λ k ) <0 (А = 0, 1, …, n -1);

• величина s= max| Re(λ k) |/min|Re(λ k) ( k= 0, 1, …, n- 1), именуемая жесткостью системы, должна быть велика.

Жесткие системы впервые появились при решении систем дифференциальных уравнений химической кинетики. Решение таких систем представляется фрагментами с сильно отличающейся крутизной зависимостей. Нередко это случается и при анализе электрических цепей с резко отличными постоянными времени.

Если шаг решения h сравним или больше наименьшей постоянной времени решения, то применение стандартных методов (например, Рунге-Кутта) с неизменным шагом приводит к большим погрешностям вычислений и даже к к расхождению вычислительного процесса, в ходе которого решение грубо отлично от существующего.

Maple в большинстве случаев дает верное решение даже без указания метода решения. Это связано с тем, что система дифференциальных уравнений при решении его функцией dsolve анализируется и в зависимости от результатов анализа выбирается наиболее подходящий метод решения. Кроме того, большинство методов (например, самый распространенный rkf45) реализуют алгоритмы контроля погрешности вычислений и дробления шага решения, если погрешность оказывается больше заданной.

В связи с указанным решение жестких систем дифференциальных уравнении средствами системы Maple не вызывает особых трудностей и может быть осуществлено даже при выборе не вполне удачного метода. Однако при этом возможны следующие ситуации:

• может резко возрасти время вычислений из за чрезмерно сильного уменьшения шага решения;

• может оказаться превышенным число итераций в ходе дробления шага;

• для «особо жестких» систем адаптивный выбор шага может не помочь и погрешность решения будет большой.

Во избежание этого рекомендуется при решении жестких систем дифференциальных уравнений все же пользоваться специально для них созданными методами, например методом Розенброка (опция method=rosenbrock для функции dsolve).

В качестве первого примера исследуем и решим следующую систему дифференциальных уравнений (файл sdes):

> deq2 := diff(u(t),t) = -11*u(t)+9*v(t), diff(v(t),t) = 9*u(t)-11*v(t);

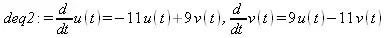
Загрузив пакет linalg вычислим собственные значения матрицы данной системы дифференциальных уравнений:

> with(linalg): M:=matrix(2,2, [-11,9,9,-11]);

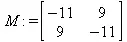
> ge:=eigenvalues(M);

Они оказались отрицательными. Кроме того, очевидно, что значение жесткости данной системы s=10. Его трудно назвать очень большим, но в целом условия жесткости для данной системы выполняются. Теперь решим эту систему методом Розенберга. Решение представлено на рис. 7.22. Обратите внимание на то, что представлены две точки и график решения. К достоинствам реализации примененного метода относится отсутствие необходимости в составлении матрицы Якоби, которую приходится задавать при использовании ряда функций системы Mathcad, имеющихся для решения жестких систем дифференциальных уравнений [9].

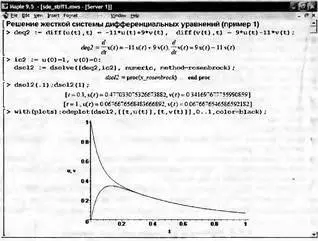
Рис. 7.22. Задание и решение жесткой системы дифференциальных уравнений (пример 1)

Еще один пример задания и решения жесткой системы дифференциальных уравнений представлен на рис. 7.23. Собственные значения матрицы этой системы равны -2 и -1000, а жесткость системы s=500 (проверьте сами по аналогии с ранее приведенным примером). Таким образом, эта система намного жестче, чем система из первого примера. Обратите внимание на то, что она решается без задания метода решения, но с опцией stiff=true, вынуждающей Maple выбирать метод для решения жестких систем дифференциальных уравнений.

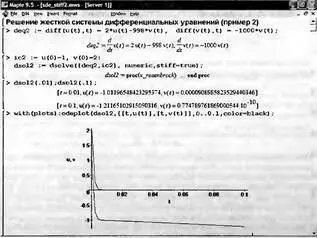
Рис. 7.23. Задание и решение жесткой системы дифференциальных уравнений (пример 2)