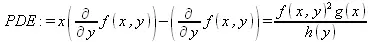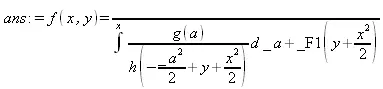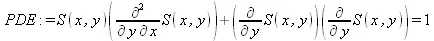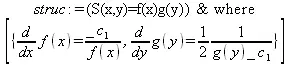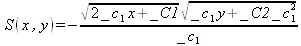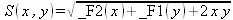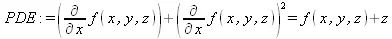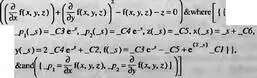Владимир Дьяконов - Maple 9.5/10 в математике, физике и образовании

В Maple 9.5 имеется функция pdsolve для решения дифференциальных уравнений с частными производными. Она может использоваться в следующих формах записи:

pdsolve(PDE, f, HINT, INTEGRATE, build)

pdsolve(PDE_system, funcs, HINT, other_options)

pdsolve(PDE_system, conds, numeric, other_options)

pdsolve(PDE_system, conds, type=numeric, other_options)

Эта функция введена вместо устаревшей функции pdesolve. В функции pdsolve используются следующие параметры:

• PDE — одиночное дифференциальное уравнение с частными производными;

• PDE system — система дифференциальных уравнений с частными производными;

• conds — начальные или граничные условия;

• f — неопределенная функция или имя;

• funcs — (опция) множество или список с неопределенными функциями или именами;

• HINT — (опция) равенство в форме HINT=argument, где аргумент может быть символом '+', '*', любым алгебраическим выражением или строкой 'strip';

• INTEGRATE — (опция) задает автоматическое интегрирование для множества ODEs (если PDE решается при разделении переменных;

• build — опция, задающая попытку построения явного выражения для неопределенной функции, независимо от общности найденного решения;

• numeric — ключевое слова, задающее решение в численном виде;

• other options — другие опции.

Для решения дифференциальных уравнений с частными производными и его визуализации в Maple 9.5 служит специальный инструментальный пакет PDEtool:

> with(PDEtools);

Ввиду небольшого числа функций этого пакета приведем их определения:

build(sol) — конструирует улучшенную форму решения, полученного функцией pdsolve;

casesplit(sys, о1, o2, …) — преобразует форму дифференциального уравнения; charstrip(PDE, f) — находит характеристическую последовательность, дающую дифференциальное уравнение первого порядка;

dchange(tr,expr,o1,o2,…) — выполняет замену переменных в математических выражениях или функциях;

dcoeff(expr,y(x)) — возвращает коэффициенты полиномиала дифференциального уравнения;

declare(expr) и др. — задает функцию для компактного ее отображения;

difforder(a,x) — возвращает порядок дифференциала в алгебраическом выражении а;

dpolyform(sys,no_Fn,opts) — возвращает полиномиальную форму для заданной системы sys не полиномиальных дифференциальных уравнений;

dsubs(deriv1=a,…,expr) — выполняет дифференциальные подстановки в выражение expr;

mapde(PDE,into,f) — создает карту PDE в различных форматах into с опциональным заданием имени неизвестной функции f;

separability(PDE, F(x,y,…), '*') — определяет условия разделения для сумм или произведений PDE;

splitstrip(PDE, f) — разделяет характеристическую последовательность на несоединенные поднаборы;

splitsys(sys,funcs) — разделяет наборы уравнений (алгебраические и дифференциальные) на несоединенные поднаборы;

undeclare(f(x),…) и др. — отменяет задание функции для компактного ее отображения.

Примеры решения дифференциальных уравнений и систем с частными производными представлены ниже (файл pde):

> restart: with(PDEtools):

> PDE := x*diff(f(x, y), y) - diff(f(x,y),x)=f(x,y;^2*g(x)/h(y);

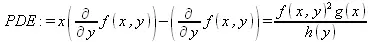
> ans := pdsolve(PDE);

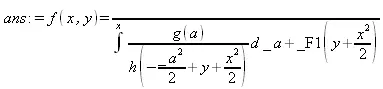
> PDE := S(x,y)*diff(S(x,y),y,x) + diff(S(x,y),x)*diff(S(x,y),y) = 1;

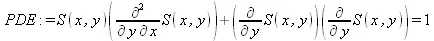
> struc := pdsolve(PDE, HINT=f(x)*g(y));

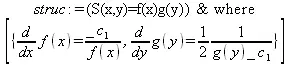
> build(struc);

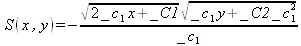
> pdsolve(PDE,HINT=P(x,y)^(1/2));

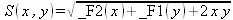
> PDE := diff(f(x,y,z), x) + diff(f(x,y,z), у)^2 = f(x,y,z)+z;

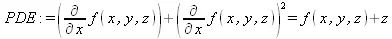
> pdsolve(PDE, HINT=strip);

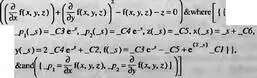
> myPDEsystem := [-y*diff(f(x,у,z,t),x) +

z^2*diff(f(x,y,z,t),z) + 3*t*z*diff(f(x,y,z,t),t) - 3*t^2-4*f(x,y,z,t)*z = 0,

-y*diff(f(x, y, z, t), y) - z*diff(f(x,y,z,t),z) -