Владимир Дьяконов - Maple 9.5/10 в математике, физике и образовании

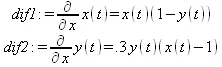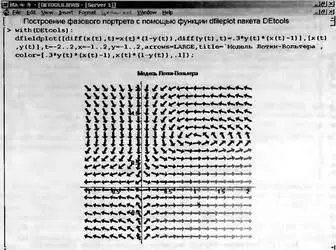
Рис. 7.18. Построение фазового портрета в виде графика векторного поля

Обратите внимание на использование опций в этом примере — в частности, на вывод надписи на русском языке. В целом список параметров функции phaseportrait аналогичен таковому для функции DEplot (отсутствует лишь задание начальных условий).

Графическая функция phaseportrait служит для построения фазовых портретов по результатам решения одного дифференциального уравнения или системы дифференциальных уравнений deqns. Она задается в следующем виде:

phaseportrait(deqns,vars,trange,inits,о)

При задании уравнений достаточно указать их правые части. На рис. 7.19 представлен пример применения функции phaseportrait для решения системы из трех дифференциальных уравнений первого порядка.

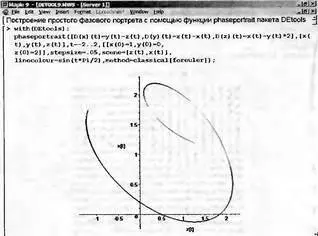
Рис. 7.19. Построение фазового портрета с помощью функции phaserportrait

В этом примере система дифференциальных уравнений задана с помощью оператора дифференцирования D. Функциональная окраска линии фазового портрета достигается использованием параметра linecolor в правой части которой задана формула для цвета.

Еще более интересный пример решения дифференциального уравнения представлен на рис. 7.20. Здесь построены фазовые портреты для асимптотических решений.

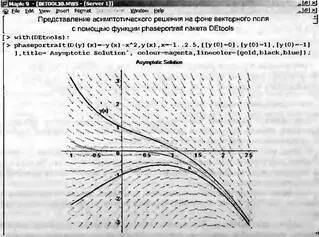
Рис. 7.20. Построение асимптотического решения на фоне графика векторного поля

В целом надо отметить, что возможности визуализации решений дифференциальных уравнений с помощью системы Maple весьма велики и приведенные выше примеры лишь частично иллюстрируют сказанное.

Maple 9.5 существенно доработан по части решения дифференциальных уравнений (ДУ) и систем с ДУ. Эта доработка, прежде всего, направлена на получение верных решений как можно большего числа ДУ разных классов и систем с ДУ. В частности расширен круг нелинейных дифференциальных уравнений, для которых система Maple 9.5 способна дать аналитические решения.

Весь арсенал средств решения ДУ и методика их применения вполне заслуживают отражения в отдельной большой книге. Мы ограничимся описанием только трех средств системы Maple — проверки ДУ на автономность, углубленным анализом решения с помощью контроля уровня выхода и получением приближенного полиномиального аналитического решения.

Одиночное дифференциальное уравнение или система дифференциальных уравнений называется автономной, если их правая часть явно не зависит от независимой переменной. Для автономных дифференциальных уравнений или систем при построении графиков решений функцией DEplot не обязательно задавать начальные условия, но нужно указывать диапазон изменения искомых переменных.

Для проверки уравнений (или систем) на автономность используется функция

autonomous(des,vars, ivar)

где des — заданное дифференциальное уравнение или (в виде списка) система дифференциальных уравнений, vars — зависимые переменные и ivar — независимая переменная. Если система автономна, то эта функция возвращает true, в противном случае false.

Примеры:

> dif1:=diff(х(t),t)=x(t)*(1-y(t));

dif2:=diff(y(t),t)=.3*y(t)*(x(t)-1);

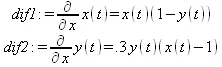
> autonomous({dif1,dif2),[x(t),y(t)],t);

> autonomous(diff(x(t),t)=sin(t),x,t);

В первом случае система дифференциальных уравнений (модель Лотки-Вольтерра) автономна, а во втором случае дифференциальное уравнение не автономно.

Для углубленного анализа аналитического решения ДУ (или системы ДУ) можно использовать специальную возможность управления уровнем вывода решения с помощью системной переменной infolevel(dsolve):=level. Значение level=all дает обычный вывод решения без комментариев, уровень 1 зарезервирован для информации, которую может сообщить пользователь, уровень 2 или 3 дает более детальный вывод (включая сообщения об использованном алгоритме и технике решения) и, наконец, уровни 4 и 5 дают наиболее детальную информацию (если таковая есть в дополнение к той информации, которую дает уровень 2 или 3).