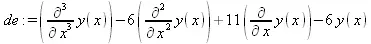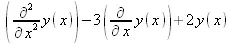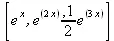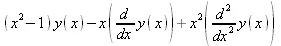Владимир Дьяконов - Maple 9.5/10 в математике, физике и образовании

Функция

reduceOrder(des,dvar,partsol, solutionForm)

обеспечивает понижение порядка дифференциального уравнения des (или системы уравнений, представленных списком или множеством) при зависимых переменных dvar, частном решении partsol (или списке частных решений) и флаге solutionForm, показывающем, что решение происходит явным методом (explicitly).

Для демонстрации действия этой функции воспользуемся примером из ее справочной страницы:

> de := diff(Y(х),х$3) - 6*diff(y(х),х$2) + 11*diff(y(х),х) - 6*y(х);

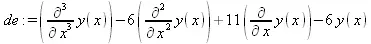
> sol:=exp(x);

> reduceOrder(de, y(х), sol);

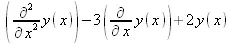
> reduceOrder(de, y(x), sol, basis);

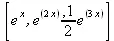
Функция

regularsp(des,ivar,dvar)

вычисляет регулярные особые (сингулярные) точки для дифференциального уравнения второго порядка или системы дифференциальных уравнений des. Следующий пример поясняет применение данной функции:

> coefs := [21*(х^2-х+1), 0, 100*х^2*(х-1)^2]:

> regularsp(coefs, х);

Еще две функции пакета DEtools

translate(des,ivar,pt,dvar)

untranslate(des,ivar,pt,dvar)

выполняют особую операцию трансляции дифференциального уравнения (или списка дифференциальных уравнений) из центрированного относительно 0 в центрированное относительно 1 и наоборот. С деталями этого специфического процесса заинтересованный читатель может познакомиться в справочной базе данных. И еще одна полезная функция пакета

varparam(sols,v,ivar)

находит общее решение дифференциального уравнения (или системы уравнений) sols методом вариации параметров. Параметр v задает правую часть уравнения; если он равен 0, ищется только частичное решение.

> varparam([u1(х), u2(х)[LDV4]], g(x), х);

Более подробную информацию об этих функциях читатель найдет в их справочных страницах, а также в информационном документе DEtools.mws, содержащем систематизированное описание пакета DEtools с многочисленными примерами его применения.

Средствами пакета DEtools предусмотрена работа с дифференциальными операторами DF, которые дают компактное представление производных, например (файл difop):

> restart; with(DEtools):

> df := x*2*DF^2 - x*DF + (х^2 - 1);

Данное выражение представляет собой дифференциальное уравнение второго порядка, записанное через дифференциальные операторы. С помощью функции diffop2de это уравнение можно преобразовать в обычное дифференциальное уравнение:

> diffop2de(df,y(x),[DF,x]);

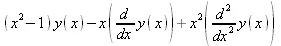
Теперь это уравнение можно решить с помощью функции dsolve :

> dsolve(%, y(x));

Уравнения с дифференциальными операторами имеет вид степенного многочлена. Поэтому с ним можно выполнять множество операций, характерных для полиномов, например факторизацию, комплектование по степеням и др. В практике инженерных и научных расчетов дифференциальные операторы применяются довольно редко. Множество примеров с ними дано в файле примеров diffop.mws.

Для обычного графического представления результатов решения дифференциальных уравнений может использоваться функция odeplot из описанного выше пакета plots. Эта функция используется в следующем виде:

odeplot(s,vars, r, о)

где s — запись (в выходной форме) дифференциального уравнения или системы дифференциальных уравнений, решаемых численно функцией dsolve, vars — переменные, r — параметр, задающий пределы решения (например, a..b) и о — необязательные дополнительные опции.

На рис. 7.11 представлен пример решения одиночного дифференциального уравнения с выводом решения у(х) с помощью функции odeplot.