Владимир Дьяконов - Maple 9.5/10 в математике, физике и образовании

│ │ 5. ││

│ │ ││

│2.,│ 3. ││

│ │ ││

│ │ ││

└ └2.50000000000000000┘┘

Ряд других подобных примеров применения функции LPSolve можно найти в справке по этой функции.

Для реализации квадратичного программирования служит функция

QPSolve(obj, constr, bd, opts)

С параметрами, описанными выше для функции LPSolve. Пример реализации квадратичного программирования представлен на рис. 6.5. Здесь оптимизируется выражение -3х²-2y², которое квадратично зависит от переменных x и у. Здесь также интересна техника визуализации квадратичного программирования.

Рис. 6.5. Пример квадратичного программирования

Эта функция также может быть записана в матричной форме:

QPSolve(obj, lc, bd, opts)

Пример применения этой функции дан ниже:

> с := Vector([2, 5.1 , datatype=float):

H := Matrix([[6, 3], [3, 4]], datatype=float):

A := Matrix([[-1,1]], datatype=float):

b := Vector([-2], datatype=float): QPSolve([с, H], [A, b]);

┌ ┌0.46666666666666564┐┐

│-3.5333333333333,│ ││

│ │-1.6000000000000030││

└ └ ┘┘

Ряд подобных примеров можно найти в справке по данной функции.

Нелинейное программирование позволяет решать задачи оптимизации при нелинейных зависимостях целевой функции от ее аргументов. Для этого в пакете Optimization имеется функция:

NLPSolve(obj, constr, bd, opts)

NLPSolve(opfobj, ineqcon, eqcon, opfbd, opts)

Ее параметры те же, что и у ранее описанных функций. В связи с этим ограничимся парой примеров ее применения при целевых функциях одной и двух переменных:

> NLESolve(х*ехр(-х), х=0..6, maximize);

> NLPSolve(х*y*ехр(-х)*ехр(-y), х=0..6, y=0..6,maximize);

В оптимизируемых функциях этих примеров присутствует экспоненциальная зависимость, что и указывает на решение задачи нелинейного программирования. Однако следует отметить, что ограничения должны быть линейными — в противном случае возвращается сообщение об ошибке с указанием на необходимость обеспечения линейности ограничивающих условий.

Возможна и матричная форма функции:

NLPSolve(n, р, nc, nlc, lc, bd, opts)

NLPSolve(n, р, lc, bd, opts)

Примеры на ее применение можно найти в справке по функции NLPSolve.

Для импорта данных из файлов служит функция:

ImportMPS(filename [, maxm, maxn, lowbnd, upbnd, opts])

В ней используются следующие параметры:

• filename — имя файла для MPS(X) в виде строки;

• maxm — максимальное число линейных ограничений;

• maxn — максимальное число переменных;

• lowbnd — значение нижней границы для переменных;

• upbnd — значение верхней границы для переменных;

• opts — выражения в виде опций, записываемых в форме option=value, где option один из объектов rhsname, rangename или boundsname, заданный для Import MPS команд.

С деталями применения этой функции можно ознакомиться по справке по ней.

Наконец в Maple 9.5 появились средства для полноценной нелинейной регрессии (реализации метод наименьших квадратов для произвольных приближающих зависимостей). Для этого служит функция:

LSSolve(obj, constr, bd, opts)

LSSolve(opfobj, ineqcon, eqcon, opfbd, opts)

Большинство ее параметров уже описывалось. Исключением является параметр opfobj — список процедур для остатков (разностей) метода наименьших квадратов. Пример применения этой функции для приближения облака заданных точек data нелинейной зависимостью с именем р дан на рис. 6.6.

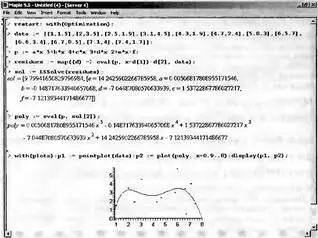
Рис. 6.6. Пример нелинейной регрессии с помощью функции LSSolve

Функция Interactive служит для организации интерактивной оптимизации в Maplet-окне. Эта функция может задаваться в виде: