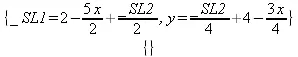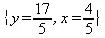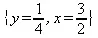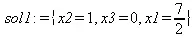Владимир Дьяконов - Maple 9.5/10 в математике, физике и образовании

Реализовывать симплекс-метод вручную — громоздко и сложно. Системы компьютерной математики имеют средства решения задач оптимизации, в том числе и симплекс-методом. Рассмотрим примеры решения несколько типичных задач линейного программирования с помощью таких средств системы Maple 9.5.

В пакете simplex системы Maple имеется небольшой, но достаточно представительный набор функций и определений для решения задач линейной оптимизации и программирования:

> with(simplex);

Warning, the protected names maximize and minimize have been redefined

and unprotected

Приведем краткое назначение этих функций:

• basis возврат списка основных переменных для множества линейных уравнений;

• convexhull — вычисление выпуклой оболочки для набора точек;

• cterm — задание констант для системы уравнений или неравенств;

• define_zero — определение наименьшего значения, принимаемого за ноль (по умолчанию увязано со значением системной переменной Digits);

• display — вывод системы уравнений или неравенств в матричной форме;

• dual — выдача сопряженных выражений;

• equality — параметр для функции convert, указывающая на эквивалентность;

• feasible — выяснение возможности решения заданной задачи:

• maximize — вычисление максимума функции;

• minimize — вычисление минимума функции;

• pivot — создание новой системы уравнений с заданным главным элементом;

• pivoteqn — выдача подсистемы уравнений для заданного главного элемента;

• pivotvar — выдача переменных с положительными коэффициентами в целевой функции;

• ratio — выдача отношений для определения наиболее жесткого ограничения;

• setup — задание системы линейных уравнений;

• standardize — приведение заданной системы уравнений или неравенств к стандартной форме неравенств типа «меньше или равно».

Главными из этих функций являются maximize и minimize, оптимизирующие задачу симплекс-методом. Они записываются в следующих формах:

maximize(f, С)

minimize(f, С)

minimize(f , С, vartype)

maximize(f , C, vartype)

maximize(f , C, vartype, 'NewC', 'transform')

minimize(f , C, vartype, 'NewC', 'transform')

Здесь f — линейное выражение, С — множество или список условий, vartype — необязательно задаваемый тип переменных NONNEGATIVE или UNRESTRICTED, NewC и transform — имена переменных, которым присваиваются соответственно оптимальное описание и переменные преобразования. Ниже даны примеры применения этих функций (файл simplex):

> restart:with(simplex):

Warning, the protected names maximize and minimize have been redefined and unprotected

> minimize(x+y, {4*x+3*y <= 5, 3*x+4*y <= 4}, NONNEGATIVE);

> minimize(x-y, {4*x+2*y <= 10, 3*x+4*y <= 16}, NONNEGATIVE, 'NC', 'vt');

> NC;vt;

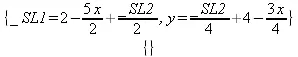
> maximize(x+y, {4*x+2*y <= 10, 3*x+4*y <= 16}, NONNEGATIVE);

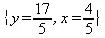
> maximize(x+y, {3*x+2*y <= 5, 2*x+4*y <=4});

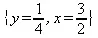
> z := 2*x1 - x2 + 3*x3;

> cnts1 := [x2+2*x3 <= 1, 2*x1-4*x2+6*x3 <= 3, -x1+3*x2+4*x3 <= 12];

> sol1 := maximize(z,cnts1,NONNEGATIVE);

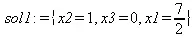
При использовании функций minimize и maximize надо не забывать, что это переопределенные функции — аналогичные по названию функции есть в ядре и они реализуют иные методы вычислений. Для возврата к исходному определению функций надо выполнить команду restart.

Функция basis(C) возвращает базис для системы линейных уравнений С. Например:

> basis([х = 2*z+w, z = 2*y-w]);

Функция convexhull(ps) возвращает выпуклую оболочку множества точек ps. Например:

> convexhull({[0,0], [1,1], [2,-1], [1,1/3],[1,1/2]));