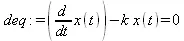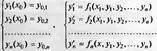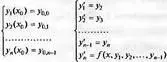Владимир Дьяконов - Maple 9.5/10 в математике, физике и образовании

Представим задание дифференциального уравнения динамики популяций по модели Мальтуса и его решение в аналитическом виде:

> restart:deq := diff(х(t),t) - k*x(t)=0;

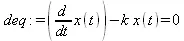
> dsol1 := dsolve({deq,x(0)=N});

Нетрудно заметить, что решение этого уравнения аналогично решению дифференциального уравнения радиоактивного распада и описывается также экспоненциальной функций. Однако, в зависимости от того, какой фактор (рождаемость или смертность) преобладает наблюдается либо экспоненциальный рост, либо экспоненциальный спад биомассы популяций.

Более правдоподобную модель популяций предложили Ферхюльст и Пирл. Эта модель учитывает (коэффициентом внутривидовую конкуренцию и позволяет учесть приближение популяций к некоторому состоянию равновесия. На рис. 7.1 представлено дифференциальное уравнение динамики популяций Ферхюльста-Пирла. Решения приведены в общем виде, а также для k=g= k/g= 1 и разных x(0)=1, 0.5 и 2.

Рис. 7.1. Моделирование популяций по модели Ферхюльста и Пирла

Поведение системы зависит от соотношения k/g и x(0)=N. При их равенстве количество биомассы популяции не меняется. При N>k/g биомасса экспоненциально уменьшается, приближаясь к значению k/g, а при N она экспоненциально возрастает, также приближаясь к k/g.

Встроенные в математические системы функции обычно решают систему из обыкновенных дифференциальных уравнений (ОДУ), представленную в форме Коши:

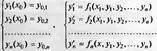
Здесь левая система задает начальные условия, а вторая представляет систему ОДУ.

Часто встречаются ДУ высокого (n-го) порядка:

где

Обозначив

и

Теперь решение этого уравнения можно свести к решению системы ОДУ:

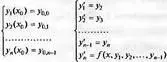
В таком виде ДУ n-го порядка может решаться стандартными средствами решения систем ОДУ, входящими в большинство математических систем.

В качестве примера аналитического решения системы дифференциальных уравнений рассмотрим постановку типичной физической задачи моделирования «Бросок камня», позволяющую описать полет камня, брошенного под углом к горизонту.

Модель должна позволять:

Вычислять положение камня в любой момент времени.

Исходные данные:

Масса камня, начальные координаты, начальная скорость и угол броска мяча.

На основе содержательной модели разрабатывается концептуальная формулировка задачи моделирования. Применительно к нашей задаче движение камня может быть описано в соответствии с законами классической механики Ньютона.

Гипотезы, принятые для модели:

• камень будем считать материальной точкой массой m, положение которой совпадает с центром масс камня;

• движение происходит в поле силы тяжести с постоянным ускорением свободного падения g и описывается уравнениями классической механики Ньютона;

• движение камня происходит в одной плоскости, перпендикулярной поверхность Земли;

• сопротивлением воздуха на первых порах пренебрегаем.

В качестве параметров движения будем использовать координаты ( х, у ) и скорость v(v x, v y) центра масс камня.

Концептуальная постановка задачи на основе принятых гипотез заключается в определении закона движения материальной точки массой m под действием силы тяжести, если известны начальные координаты точки х 0и ее начальная скорость v 0и угол броска α 0.

Таким образом, модель является простой — объект, как материальная точка, не имеет внутренней структуры. Учитывая типичные скорости и высоту броска камня, можно считать постоянным ускорение свободного падения. Переход от трехмерных координат к плоскости значительно упрощает решение задачи. Он вполне допустим, если камень не подкручивается при броске. Пренебрежение сопротивлением воздуха, как будет показано далее, приводит к значительной систематической ошибке результатов моделирования.