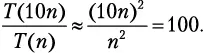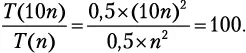Владстон Феррейра Фило - Теоретический минимум по Computer Science [Все что нужно программисту и разработчику]
Здесь есть возможность читать онлайн «Владстон Феррейра Фило - Теоретический минимум по Computer Science [Все что нужно программисту и разработчику]» — ознакомительный отрывок электронной книги совершенно бесплатно, а после прочтения отрывка купить полную версию. В некоторых случаях можно слушать аудио, скачать через торрент в формате fb2 и присутствует краткое содержание. Город: СПб., Год выпуска: 2018, ISBN: 2018, Издательство: Питер, Жанр: Программирование, Прочая околокомпьтерная литература, на русском языке. Описание произведения, (предисловие) а так же отзывы посетителей доступны на портале библиотеки ЛибКат.
- Название:Теоретический минимум по Computer Science [Все что нужно программисту и разработчику]
- Автор:
- Издательство:Питер
- Жанр:
- Год:2018
- Город:СПб.
- ISBN:978-5-4461-0587-8
- Рейтинг книги:4 / 5. Голосов: 1
-
Избранное:Добавить в избранное
- Отзывы:
-
Ваша оценка:
Теоретический минимум по Computer Science [Все что нужно программисту и разработчику]: краткое содержание, описание и аннотация
Предлагаем к чтению аннотацию, описание, краткое содержание или предисловие (зависит от того, что написал сам автор книги «Теоретический минимум по Computer Science [Все что нужно программисту и разработчику]»). Если вы не нашли необходимую информацию о книге — напишите в комментариях, мы постараемся отыскать её.
Владстон Феррейра Фило знакомит нас с вычислительным мышлением, позволяющим решать любые сложные задачи. Научиться писать код просто — пара недель на курсах, и вы «программист», но чтобы стать профи, который будет востребован всегда и везде, нужны фундаментальные знания. Здесь вы найдете только самую важную информацию, которая необходима каждому разработчику и программисту каждый день. cite
Владстон Феррейра Фило
![Владстон Феррейра Фило Теоретический минимум по Computer Science [Все что нужно программисту и разработчику] обложка книги](/books/389524/vladston-ferrejra-filo-teoreticheskij-minimum-po-co-cover.webp)

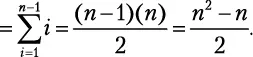
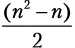 раз, отсюда n 2— n операций. В целом стоимость алгоритма 2 n — n складывается из операций внешнего цикла и n 2операций внутреннего цикла. Мы получаем временную сложность:
раз, отсюда n 2— n операций. В целом стоимость алгоритма 2 n — n складывается из операций внешнего цикла и n 2операций внутреннего цикла. Мы получаем временную сложность: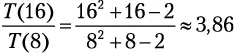 .
. Вчера вы опрокинули коробку с учетными карточками, и вам пришлось потратить два часа на сортировку выбором, чтобы все исправить. Сегодня вы рассыпали 10 коробок. Сколько времени вам потребуется, чтобы расставить карточки в исходном порядке?
Вчера вы опрокинули коробку с учетными карточками, и вам пришлось потратить два часа на сортировку выбором, чтобы все исправить. Сегодня вы рассыпали 10 коробок. Сколько времени вам потребуется, чтобы расставить карточки в исходном порядке?