1 ...7 8 9 11 12 13 ...66 Перечисленные события несовместны: нельзя выбрать и основной, и профессиональный тарифы одновременно . Вероятность, что пользователь подпишется на платный тариф, равняется 0,2 + 0,1 = 0,3.
Взаимодополняющие события
Выпавшее на кубике количество очков не может одновременно оказаться кратным трем (3, 6) и не делящимся на три, но оно определенно будет относиться к одной из этих категорий чисел. Вероятность получить результат, кратный трем, равняется 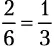 , следовательно, вероятность получить число, которое не делится на три, равняется
, следовательно, вероятность получить число, которое не делится на три, равняется 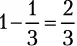 . Когда два несовместных события охватывают все возможные варианты, их называют взаимодополняющими , или соподчиненными. Сумма вероятностей взаимодополняющих событий равна 100 %.
. Когда два несовместных события охватывают все возможные варианты, их называют взаимодополняющими , или соподчиненными. Сумма вероятностей взаимодополняющих событий равна 100 %.
Игра «Защита башни»  Ваш замок защищен пятью башнями. Каждая имеет 20 %-ную вероятность поразить захватчика, прежде чем он достигнет ворот. Каковы шансы остановить его?
Ваш замок защищен пятью башнями. Каждая имеет 20 %-ную вероятность поразить захватчика, прежде чем он достигнет ворот. Каковы шансы остановить его?
Вероятность поразить врага равна 0,2 + 0,2 + 0,2 + 0,2 + 0,2 = 1, или 100 %, верно? Неверно! Никогда не суммируйте вероятности независимых событий, не совершайте распространенной ошибки. Вместо этого используйте взаимодополняющие события дважды следующим образом.
• 20 %-ный шанс поразить врага — взаимодополняющий для 80 %-го шанса промахнуться. Вероятность того, что не попадут все башни, составляет 0,8 5≈ 0,33.
• Событие «все башни промахнулись» — взаимодополняющее для события «по крайней мере одна башня попала». Значит, вероятность остановить врага равна 1–0,33 = 0,67.
Если вы подбросили монету 10 раз и получили 10 «орлов», увеличилась ли от этого вероятность, что на 11-м броске выпадет «решка»? Или будет ли вероятность выигрыша в лотерею комбинации из шести последовательных чисел от 1 до 6 ниже, чем любой другой комбинации?
Не становитесь жертвой «заблуждения игрока»! Уже случившееся никак не влияет на результат независимого события. Никак. Никогда. В по-настоящему случайно разыгрываемой лотерее вероятность выпадения любого конкретного числа точно такая же, как любого другого. Нет никакой закономерности, согласно которой числа, редко выпадавшие в прошлом, должны чаще выпадать в будущем.
Более сложные вероятности
Можно было бы и дальше рассказывать о вероятности, но рамки раздела не позволяют этого. Всегда, занимаясь решением сложных задач, подыскивайте дополнительные инструменты. Вот пример.
И еще одно формирование команды  23 человека хотят в вашу команду. В отношении каждого вы подбрасываете монету и принимаете его, только если выпадает «орел». Каковы шансы, что вы возьмете семь человек или меньше?
23 человека хотят в вашу команду. В отношении каждого вы подбрасываете монету и принимаете его, только если выпадает «орел». Каковы шансы, что вы возьмете семь человек или меньше?
Да, это трудно посчитать. Если вы будете долго искать в Интернете, то в конечном счете придете к биномиальному распределению. Вы можете визуализировать его в Wolfram Alpha [21] См. http://wolframalpha.com .
, набрав: B(23,l/2) <= 7.
В этой главе мы увидели приемы решения задач, не связанные с программированием непосредственно.
Раздел 1.1 объяснил, почему и как мы должны излагать мысли в письменной форме. Для наших задач мы создаем модели и применяем к ним концептуальные инструменты.
Раздел 1.2 познакомил с инструментами из булевой алгебры для работы с формальной логикой и таблицами истинности.
Раздел 1.3 показал важность теории вероятности и комбинаторики для решения задач разного рода. Быстрый приблизительный подсчет может показать вам, стоит ли браться за дальнейшие вычисления. Программисты-новички часто теряют время, анализируя слишком много сценариев.
Наконец, раздел 1.4 объяснил основные правила, позволяющие подсчитать вероятность чего-либо. Это бывает очень полезно при разработке решений, которые должны взаимодействовать с нашим дивным, но неопределенным миром.
Таким образом, мы в общих чертах обрисовали множество важных аспектов того, что ученые называют дискретной математикой. Еще больше интересного можно почерпнуть из приведенных ниже материалов или просто найти в «Википедии». Например, вы можете воспользоваться принципом Дирихле, чтобы доказать, что в Нью-Йорке по крайней мере у двух человек одинаковое число волос в шевелюре!
Читать дальше
Конец ознакомительного отрывка
Купить книгу
![Владстон Феррейра Фило Теоретический минимум по Computer Science [Все что нужно программисту и разработчику] обложка книги](/books/389524/vladston-ferrejra-filo-teoreticheskij-minimum-po-co-cover.webp)
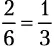 , следовательно, вероятность получить число, которое не делится на три, равняется
, следовательно, вероятность получить число, которое не делится на три, равняется 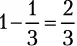 . Когда два несовместных события охватывают все возможные варианты, их называют взаимодополняющими , или соподчиненными. Сумма вероятностей взаимодополняющих событий равна 100 %.
. Когда два несовместных события охватывают все возможные варианты, их называют взаимодополняющими , или соподчиненными. Сумма вероятностей взаимодополняющих событий равна 100 %. Ваш замок защищен пятью башнями. Каждая имеет 20 %-ную вероятность поразить захватчика, прежде чем он достигнет ворот. Каковы шансы остановить его?
Ваш замок защищен пятью башнями. Каждая имеет 20 %-ную вероятность поразить захватчика, прежде чем он достигнет ворот. Каковы шансы остановить его? 23 человека хотят в вашу команду. В отношении каждого вы подбрасываете монету и принимаете его, только если выпадает «орел». Каковы шансы, что вы возьмете семь человек или меньше?
23 человека хотят в вашу команду. В отношении каждого вы подбрасываете монету и принимаете его, только если выпадает «орел». Каковы шансы, что вы возьмете семь человек или меньше?









