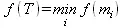Иван Братко - Программирование на языке Пролог для искусственного интеллекта

f( n) = g( n) + h( n)

Для дерева T с корнем n , имеющем преемников m 1, m 2, …, получаем

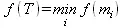
Программа поиска с предпочтением, составленная в соответствии с приведенными выше общими соображениями, показана на рис 12.3. Ниже даются некоторые дополнительные пояснения.

Так же, как и в случае поиска в ширину (рис. 11.13), ключевую роль играет процедура расширить, имеющая на этот раз шесть аргументов:

расширить( Путь, Дер, Предел, Дер1, ЕстьРеш, Решение)

Эта процедура расширяет текущее (под)дерево, пока f -оценка остается равной либо меньшей, чем Предел.

% Поиск с предпочтением

эврпоиск( Старт, Решение) :-

макс_f( Fмакс). % Fмакс > любой f-оценки

расширить( [], л( Старт, 0/0), Fмакс, _, да, Решение).

расширить( П, л( В, _ ), _, _, да, [В | П] ) :-

цель( В).

расширить( П, л( В, F/G), Предел, Дер1, ЕстьРеш, Реш) :-

F <= Предел,

( bagof( B1/C, ( после( В, В1, С), not принадлежит( В1, П)),

Преемники), !,

преемспис( G, Преемники, ДД),

опт_f( ДД, F1),

расширить( П, д( В, F1/G, ДД), Предел, Дер1,

ЕстьРеш, Реш);

ЕстьРеш = никогда). % Нет преемников - тупик

расширить( П, д( В, F/G, [Д | ДД]), Предел, Дер1,

ЕстьРеш, Реш) :-

F <= Предел,

опт_f( ДД, OF), мин( Предел, OF, Предел1),

расширить( [В | П], Д, Предел1, Д1, ЕстьРеш1, Реш),

продолжить( П, д( В, F/G, [Д1, ДД]), Предел, Дер1,

ЕстьРеш1, ЕстьРеш, Реш).

расширить( _, д( _, _, []), _, _, никогда, _ ) :- !.

% Тупиковое дерево - нет решений

расширить( _, Дер, Предел, Дер, нет, _ ) :-

f( Дер, F), F > Предел. % Рост остановлен

продолжить( _, _, _, _, да, да, Реш).

продолжить( П, д( В, F/G, [Д1, ДД]), Предел, Дер1,

ЕстьРеш1, ЕстьРеш, Реш) :-

( ЕстьРеш1 = нет, встав( Д1, ДД, НДД);

ЕстьРеш1 = никогда, НДД = ДД),

опт_f( НДД, F1),

расширить( П, д( В, F1/G, НДД), Предел, Дер1,

ЕстьРеш, Реш).

преемспис( _, [], []).

преемспис( G0, [В/С | ВВ], ДД) :-

G is G0 + С,

h( В, H), % Эвристика h(B)

F is G + H,

преемспис( G0, ВВ, ДД1),

встав( л( В, F/G), ДД1, ДД).

% Вставление дерева Д в список деревьев ДД с сохранением

% упорядоченности по f-оценкам

встав( Д, ДД, [Д | ДД] ) :-

f( Д, F), опт_f( ДД, F1),

F =< F1, !.

встав( Д, [Д1 | ДД], [Д1 | ДД1] ) ) :-

встав( Д, ДД, ДД1).

% Получение f-оценки

f( л( _, F/_ ), F). % f-оценка листа

f( д( _, F/_, _ ) F). % f-оценка дерева

опт_f( [Д | _ ], F) :- % Наилучшая f-оценка для

f( Д, F). % списка деревьев

опт_f( [], Fмакс) :- % Нет деревьев:

мaкс_f( Fмакс). % плохая f-оценка

мин( X, Y, X) :-

X =< Y, !.

мин( X, Y, Y).

Рис. 12.3. Программа поиска с предпочтением.

Аргументы процедуры расширитьимеют следующий смысл:

Переменные Путь, Дер, и Предел — это "входные" параметры процедуры расширитьв том смысле, что при каждом обращении к расширитьони всегда конкретизированы. Процедура расширитьпорождает результаты трех видов. Какой вид результата получен, можно определить по значению индикатора ЕстьРешследующим образом:

(1) ЕстьРеш = да

Решение= решающий путь, найденный при расширении дерева Дерс учетом ограничения Предел.

Дер1= неконкретизировано.

(2) ЕстьРеш = нет

Дер1= дерево Дер, расширенное до тех пор, пока его f -оценка не превзойдет Предел(см. рис. 12.4).