Иван Братко - Программирование на языке Пролог для искусственного интеллекта

• Поиск в ширину всегда первым обнаруживает самое короткое решение, что не верно в отношении стратегии поиска в глубину.

• В случае обширных пространств состояний существует опасность комбинаторного взрыва . Обе стратегии плохо приспособлены для борьбы с этой трудностью. В таких случаях необходимо руководствоваться эвристиками.

• В этой главе были введены следующие понятия:

пространство состояний

стартовая вершина, целевое условие,

решающий путь

стратегия поиска

поиск в глубину, поиск в ширину

эвристический поиск.

Поиск в глубину и поиск в ширину — базовые стратегии поиска, они описаны в любом учебнике по искусственному интеллекту, см., например, Nilsson (1971, 1980) или Winston (1984). P. Ковальский в своей книге Kowalski (1980) показывает, как можно использовать аппарат математической логики для реализации этих принципов.

Kowalski R. (1980). Logic for Problem Solving. North-Holland.

Nilsson N. J. (1971). Problem Solving Methods in Artificial Intelligence. McGraw-Hill.

Nilsson N. J. (1980). Principles of Artificial Intelligence. Tioga; also Springer-Verlag, 1981.

Winston P. H. (1984). Artificial Intelligence (second edition). Addison-Wesley. [Имеется перевод первого издания: Уинстон П. Искусственный интеллект. — М.: Мир, 1980.]

Поиск в графах при решении задач, как правило, невозможен без решения проблемы комбинаторной сложности, возникающей из-за быстрого роста числа альтернатив. Эффективным средством борьбы с этим служит эвристический поиск.

Один из путей использования эвристической информации о задаче — это получение численных эвристических оценок для вершин пространства состояний. Оценка вершины указывает нам, насколько данная вершина перспективна с точки зрения достижения цели. Идея состоит в том, чтобы всегда продолжать поиск, начиная с наиболее перспективной вершины, выбранной из всего множества кандидатов. Именно на этом принципе основана программа поиска с предпочтением, описанная в данной главе.

Программу поиска с предпочтением можно получить как результат усовершенствования программы поиска в ширину (рис. 11.13). Подобно поиску в ширину, поиск с предпочтением начинается со стартовой вершины и использует множество путей-кандидатов. В то время, как поиск в ширину всегда выбирает для продолжения самый короткий путь (т.е. переходит в вершины наименьшей глубины), поиск с предпочтением вносит в этот принцип следующее усовершенствование: для каждого кандидата вычисляется оценка и для продолжения выбирается кандидат с наилучшей оценкой.

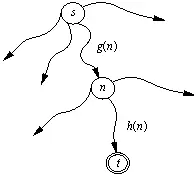
Рис. 12.1. Построение эвристической оценки f ( n ) стоимости самого дешевого пути из s в t , проходящего через n : f ( n ) = g ( n ) + h ( n ).

Мы будем в дальнейшем предполагать, что для дуг пространства состояний определена функция стоимости с ( n , n' ) — стоимость перехода из вершины n к вершине-преемнику n' .

Пусть f — это эвристическая оценочная функция, при помощи которой мы получаем для каждой вершины n оценку f ( n ) трудности" этой вершины. Тогда наиболее перспективной вершиной-кандидатом следует считать вершину, для которой f принимает минимальное значение. Мы будем использовать здесь функцию f специального вида, приводящую к хорошо известному А*-алгоритму. Функция f ( n ) будет построена таким образом, чтобы давать оценку стоимости оптимального решающего пути из стартовой вершины s к одной из целевых вершин при условии, что этот путь проходит через вершину n . Давайте предположим, что такой путь существует и что t — это целевая вершина, для которой этот путь минимален. Тогда оценку f ( n ) можно представить в виде суммы из двух слагаемых (рис. 12.1):

f ( n ) = g ( n ) + h ( n )

Здесь g ( n ) — оценка оптимального пути из s в n ; h ( n ) — оценка оптимального пути из n в t .

Когда в процессе поиска мы попадаем в вершину n , мы оказываемся в следующей ситуация: путь из s в n уже найден, и его стоимость может быть вычислена как сумма стоимостей составляющих его дуг. Этот путь не обязательно оптимален (возможно, существует более дешевый, еще не найденный путь из s в n ), однако стоимость этого пути можно использовать в качестве оценки g ( n ) минимальной стоимости пути из s в n . Что же касается второго слагаемого h ( n ), то о нем трудно что-либо сказать, поскольку к этому моменту область пространства состояний, лежащая между n и t , еще не "изучена" программой поиска. Поэтому, как правило, о значении h ( n ) можно только строить догадки на основании эвристических соображений, т.е. на основании тех знаний о конкретной задаче, которыми обладает алгоритм. Поскольку значение h зависит от предметной области, универсального метода для его вычисления не существует. Конкретные примеры того, как строят эти "эвристические догадки", мы приведем позже. Сейчас же будем считать, что тем или иным способом функция h задана, и сосредоточим свое внимание на деталях нашей программы поиска с предпочтением.