Иван Братко - Программирование на языке Пролог для искусственного интеллекта

Можно представлять себе поиск с предпочтением следующим образом. Процесс поиска состоит из некоторого числа конкурирующих между собой подпроцессов, каждый из которых занимается своей альтернативой, т.е. просматривает свое поддерево. У поддеревьев есть свои поддеревья, их просматривают подпроцессы подпроцессов и т.д. В каждый данный момент среди всех конкурирующих процессов активен только один — тот, который занимается наиболее перспективной к настоящему моменту альтернативой, т.е. альтернативой с наименьшим значением f . Остальные процессы спокойно ждут того момента, когда f -оценки изменятся и в результате какая-нибудь другая альтернатива станет наиболее перспективной. Тогда производится переключение активности на эту альтернативу. Механизм активации-дезактивации процессов функционирует следующим образом: процесс, работающий над текущей альтернативой высшего приоритета, получает некоторый "бюджет" и остается активным до тех пор, пока его бюджет не исчерпается. Находясь в активном состоянии, процесс продолжает углублять свое поддерево. Встретив целевую вершину, он выдает соответствующее решение. Величина бюджета, предоставляемого процессу на данный конкретный запуск, определяется эвристической оценкой конкурирующей альтернативы, ближайшей к данной.

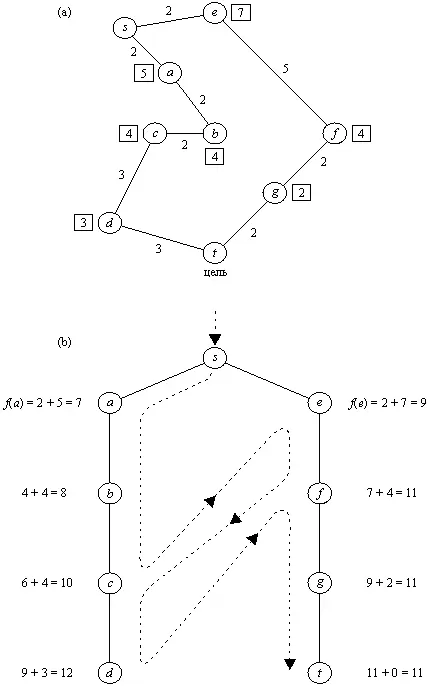
Рис. 12.2. Поиск кратчайшего маршрута из s в t . (а) Карта со связями между городами; связи помечены своими длинами; в квадратиках указаны расстояния по прямой до цели t . (b) Порядок, в котором при поиске с предпочтением происходит обход городов. Эвристические оценки основаны на расстояниях по прямой. Пунктирной линией показано переключение активности между альтернативными путями. Эта линия задает тот порядок, в котором вершины принимаются для продолжения пути, а не тот порядок, в котором они порождаются.

На рис. 12.2 показан пример поведения конкурирующих процессов. Дана карта, задача состоит в том, чтобы найти кратчайший маршрут из стартового города s в целевой город t . В качестве оценки стоимости остатка маршрута из города X до цели мы будем использовать расстояние по прямой расст( X, t) от X до t . Таким образом,

f( X) = g( X) + h( X) = g( X) + расст( X, t)

Мы можем считать, что в данном примере процесс поиска с предпочтением состоит из двух процессов. Каждый процесс прокладывает свой путь — один из двух альтернативных путей: Процесс 1 проходит через а . Процесс 2 — через e . Вначале Процесс 1 более активен, поскольку значения f вдоль выбранного им пути меньше, чем вдоль второго пути. Когда Процесс 1 достигает города с , а Процесс 2 все еще находится в e , ситуация меняется:

f( с) = g( c) + h( c) = 6 + 4 = 10

f( e) = g( e) + h( e) = 2 + 7 = 9

Поскольку f( e) < f( c) , Процесс 2 переходит к f , a Процесс 1 ждет. Однако

f( f) = 7 + 4 = 11

f( c) = 10

f( c) < f( f)

Поэтому Процесс 2 останавливается, а Процессу 1 дается разрешение продолжать движение, но только до d , так как f( d) = 12 > 11 . Происходит активация Процесса 2, после чего он, уже не прерываясь, доходит до цели t .

Мы реализуем этот механизм программно при помощи усовершенствования программы поиска в ширину (рис. 11.13). Множество путей-кандидатов представим деревом. Дерево будет изображаться в программе в виде терма, имеющего одну из двух форм:

(1) л( В, F/G) — дерево, состоящее из одной вершины (листа); В — вершина пространства состояний, G — g ( B) (стоимость уже найденного пути из стартовой вершины в В); F - f ( В) = G + h ( В).

(2) д( В, F/G, Пд) — дерево с непустыми поддеревьями; В — корень дерева, Пд — список поддеревьев; G — g ( B) ; F — уточненное значение f ( В) , т.е. значение f для наиболее перспективного преемника вершины В; список Пдупорядочен в порядке возрастания f -оценок поддеревьев.

Уточнение значения f необходимо для того, чтобы дать программе возможность распознавать наиболее перспективное поддерево (т.е. поддерево, содержащее наиболее перспективную концевую вершину) на любом уровне дерева поиска. Эта модификация f -оценок на самом деле приводит к обобщению, расширяющему область определения функции f . Теперь функция f определена не только на вершинах, но и на деревьях. Для одновершинных деревьев (листов) n остается первоначальное определение