Валентин Арьков - Эконометрические оценки. Учебное пособие

Теория объясняет общие законы природы. Там, где есть случайность, можно говорить о вероятности события.

Вероятность обозначается латинской буквой p . Это первая буква английского слова probability . Происходит от латинского слова proba – «пробовать, проверять». Получается, что один раз попробовал что-то сделать – получилось, в другой раз попробовал – не получилось. Когда мы что-то пробуем, появляется случайность, неопределённость, непредсказуемость. И вероятность – это частота события, насколько часто происходит то, что нас интересует.

Русское слово «вероятность» имеет отношению к слову «верить». И это вторая сторона вероятности: насколько мы доверяем какому-то сообщению, утверждению, прогнозу.

Рис. Вероятность: теория и оценка

Теория – это всегда красиво и всегда «точно». Теория вероятности говорит нам: если шансы равны, то вероятность будет ровно 0,5 для орла и ровно 0,5 для решки. Это абсолютно «точное» значение – никаких сомнений. Но с одной оговоркой: если шансы равны, см. рис.

Статистика – это фактические данные. Когда мы переходим к обработке данных, то никогда не видим идеальные числа и идеальные условия. Мы каждый раз видим реальные наборы данных. Например, тысячу раз бросили монетку. Посчитали, сколько раз выпал орёл. Представим, что из десяти тысяч раз почти в половине случаев монетка упала орлом вверх. Делим на общее число бросаний и получаем число, которое будет приближаться вот к теоретическому значению.

Это число называется ОЦЕНКА. Оценки часто обозначают символом «крышечка» или «крышка». Настоящая вероятность и оценка по реальным данным приблизительно соответствуют друг другу, но только ПРИБЛИЗИТЕЛЬНО. Оценку мы можем посчитать: берём реальные данные и считаем. Такие опыты были в истории. В книгах можно найти упоминание о том, как ещё до появления компьютеров математики решили проверить свои теории. Они 10 тысяч раз бросали монетку. Можете представить, какая это работа. Бросать монетку и каждый раз записывать результат на бумаге, а потом вычислить оценку вероятности.

Рис. Эксперименты и оценки

Вот в чём разница между теорией и обработкой данных. Теория говорит нам, как всё должно быть в принципе, при идеальных условиях. На практике мы берём реальные данные и обсчитываем то, что получили. Если у нас были разумные предположение, то результаты будут соответствовать теории.

Когда мы говорим о реальных данных, опыт с монеткой можно провести «физически» – действительно бросать монетку много раз. Есть и другой вариант – использовать программный генератор случайных чисел. В этом случае мы имеем дело с тем, что называется ИМИТАЦИОННОЕ МОДЕЛИРОВАНИЕ. Это целая технология, но мы с вами затронем эту область только для того, чтобы увидеть, как это происходит. Мы будем моделировать идеальные, красивые данные, на которых можно тренироваться. Потом, на лабораторных работах можно будет взять реальные, настоящие данные. Они уже не такие «красивые». Они могут быть «корявыми», «неправильными», какими угодно. Но они чем-то будут напоминать нашу теорию и наши результаты.

В любом случае, мы можем взять реальные данные или результаты моделирования. То, что мы по ним посчитаем, каждый раз будет называться ОЦЕНКА. Оценка – это очень приблизительное значение, которое может соответствовать настоящему, теоретическому.

Есть разные способы моделирования, генерирования, создания случайных чисел. Пока в качестве инструмента для работы мы обсуждаем табличный редактор – Excel или его аналоги. Первый вариант – генератор случайных чисел в настройке «Анализ данных», см. рис.

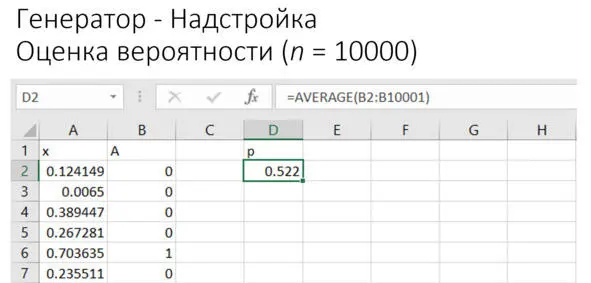
Рис. Моделирование с помощью надстройки

Мы просто генерируем столбец чисел и определяем вероятность того, что выпадет орёл. В нашем случае получилось значение 0,522. Мы как бы «бросали монетку» заданное количество раз. Генератор случайных чисел создаёт число от нуля до единицы. Эти числа имеют равномерное распределение, то есть у нас одинаковые шансы (вероятность) появления любого числа от нуля до единицы. Далее мы берём полученное число и используем функцию округления. Как вы знаете, обычно округляют по стандартному правилу. Если число меньше 0,5 – округляем в меньшую сторону и пишем 0. Если число больше 0,5 – округляем в большую сторону и пишем 1. Таким образом, мы половина чисел округляется до нуля, а другая половина чисел округляется до единицы. Если ровно 0,5 – то в большую сторону.