Роман Зыков - Роман с Data Science. Как монетизировать большие данные [litres]

До Фишера распределение в таких экспериментах производилось систематически, что могло искажать результаты. Интересно, что многие ученые не сразу приняли его метод, считая свой систематический подход верным. Кроме обычных A/Б-тестов, Фишер предложил схемы для более сложных многофакторных тестов. На деле даже с обычными тестами с двумя группами часто возникают проблемы, и до многофакторных тестов, когда проверяется сразу несколько изменений одновременно, редко кто доходит. Поэтому в этой книге я буду фокусироваться на самых простых тестах с двумя группами.

Итак, для проведения теста нам нужны метрика и рандомизация. Тесты проводят с контрольной группой. В медицине группу пациентов делят случайно на две – первой группе дают исследуемое лекарство, второй – лекарство-пустышку под названием плацебо. В маркетинге делается аналогично. Во времена почтовой торговли промоскидки отправляли одной группе клиентов, письма-пустышки (без скидок) – второй. При рассылке email-сообщений интернет-магазина контрольной группе обычно не отправляют ничего. Amazon.com, который был пионером тестирования в интернете, использовал А/Б-тесты (split test) для показа одной группе пользователей старой версии сайта, а второй – новой, и сравнивал их поведение, чтобы выбрать лучшую версию. Перед запуском полноценного боевого теста нужно проверить весь механизм работы, делается это с помощью симуляционного и реального тестов. Также можно использовать А/А-тесты – расскажу о них далее.

Для статистической проверки гипотез нам понадобится два важных понятия – генеральная совокупность и выборка. Генеральная совокупность (general population) – это все объекты, относительно которых нужно сделать выводы в исследовании. Выборка (sample) – это часть объектов генеральной совокупности, которые мы смогли пронаблюдать.

Пусть у нас есть огромный резервуар с шарами разного диаметра. В самом резервуаре сотни тысяч шаров. Средний диаметр неизвестен, и нам нужно его определить. Весь резервуар посчитать невозможно, слишком много работы нужно затратить. Для экономии средств и времени мы сделаем случайную выборку с замещением (возвращаем шар обратно после определения диаметра) определенного количества шаров. В этой задаче резервуар с шарами – это генеральная совокупность, средний диаметр шара – неизвестный параметр, который нам нужно определить, и мы сделаем это с помощью случайной выборки. Параметр в генеральной совокупности является истинным, параметр выборки является его оценкой.

Когда я слышу слово «распределение» – представляю себе гистограмму частот появления значений. В нашем примере это будет гистограмма с диаметрами шаров. Мы работаем с непрерывными числовыми значениями, вся шкала гистограммы разбивается на диапазоны, как правило, равной длины (0–10, 10.01–20…). На основе гистограммы сложно принимать решения, поэтому в гипотезах обычно оценивают какой-то отдельный параметр распределения, например среднее или медиану. Строим по ним гистограмму (рис. 10.1).

Такие гистограммы (распределения) очень сложно сравнить друг с другом, поэтому и используются числовые статистики распределений.

Генеральная совокупность имеет свое распределение шаров, выборка – свое. Чем больше выборочное распределение похоже на распределение генеральной совокупности – тем лучше. Случайность вытаскивания шаров очень важна для этого – ведь шары в резервуар могли насыпать сначала одного диаметра, потом другого. Тогда на поверхности могут оказаться самые большие шары, и если мы их будем брать преимущественно оттуда, то наше распределение шаров внутри выборки окажется смещенным в сторону большего диаметра, поэтому наши выводы могут оказаться неверными.

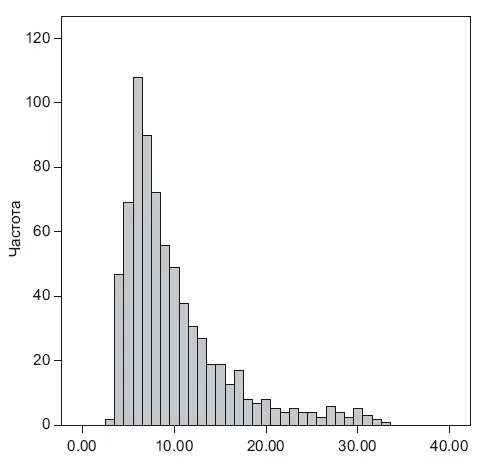
Рис. 10.1.Пример распределения

Возвращать шары нужно, чтобы работать с исходным распределением генеральной совокупности, так как каждое вытягивание будет независимо от предыдущих. Теперь давайте применим интуицию – чем больше шаров мы вытянем, тем лучше распределение выборки будет похоже на распределение в резервуаре, и тем выше точность оценки параметра в выборке мы получим. А сколько нужно вытянуть шаров, чтобы получить приемлемую точность? На этот вопрос уже ответит статистика – об этом чуть позже, а сейчас усложним задачу.