Джон Келлехер - Наука о данных. Базовый курс

Прародителем большинства современных алгоритмов машинного обучения деревьев решений является алгоритм ID3 {3} . Он строит деревья решений рекурсивным способом в глубину, добавляя один узел зараз, начиная с корневого узла. ID3 начинается с выбора атрибута для проверки в корневом узле. Ветвь вырастает для каждого значения из области определения этого тестового атрибута и помечается этим значением. Узел с бинарным тестовым атрибутом будет иметь две ветви, исходящие от него. Затем набор данных разделяется: каждый объект из этого набора перемещается вниз по той ветви, метка которой соответствует значению тестового атрибута для объекта. Затем ID3 наращивает каждую ветвь, используя тот же процесс, что и для создания корневого узла: выбрать тестовый атрибут — добавить узел с ветвями — разделить данные, направив объекты по соответствующим ветвям. Этот процесс повторяется до тех пор, пока все объекты каждой ветви не будут иметь одинаковое значение целевого атрибута, тогда в дерево добавляется конечный узел и помечается значением целевого атрибута, общего для всех объектов ветви [22].

ID3 выбирает атрибут для тестирования в каждом узле дерева, чтобы минимизировать количество тестов, необходимых для создания очищенных наборов (т. е. таких групп объектов, которые имеют одинаковое значение целевого атрибута). Одним из способов измерения чистоты набора является использование информационной энтропии — меры неопределенности информации Клода Шеннона. Минимально возможная энтропия для множества равна нулю, поэтому очищенное множество имеет энтропию, равную нулю. Максимальное значение возможной энтропии для набора зависит от его размера и разнообразия представленных типов элементов. Набор будет иметь максимальную энтропию, когда все элементы в нем разного типа [23]. ID3 выбирает для тестирования в узле атрибут, который приводит к наименьшему значению взвешенной энтропии после разделения набора данных с использованием этого атрибута. Взвешенная энтропия для атрибута рассчитывается следующим путем: 1) разделение набора данных по атрибуту; 2) вычисление энтропии результирующих множеств; 3) взвешивание каждой энтропии по ее доле в наборе данных; 4) суммирование результатов.

В табл. 3 приведен список электронных писем, в котором каждое описывается рядом атрибутов и тем, является оно спамом или нет. Атрибут «Вложение» имеет значение «Истина» для электронных писем, содержащих вложение, и значение «Ложь» в ином случае (в этой выборке ни одно из электронных писем не имело вложений). Атрибут «Подозрительные слова» имеет значение «Истина», если электронное письмо содержит одно или несколько слов в предварительно определенном списке подозрительных слов. Атрибут «Неизвестный отправитель» истинен, если отправитель электронного письма отсутствует в адресной книге получателя. Этот набор данных использовался для обучения дерева решений на рис. 16. В нем атрибуты «Вложение», «Подозрительные слова» и «Неизвестный отправитель» были входными атрибутами, а атрибут «Спам» — целью. Атрибут «Неизвестный отправитель» разбивает набор данных на более чистые группы, чем другие атрибуты (одна из них содержит большинство объектов, где Спам = Истина, а другая, где Спам = Ложь). Затем «Неизвестный отправитель» помещается в корневой узел, как на рис. 17. После этого начального разделения все объекты в правой ветви имеют одинаковое целевое значение, а объекты в левой — разное. Разделение объектов в левой ветви с использованием атрибута «Подозрительные слова» приводит к образованию двух чистых наборов, где также для одного Спам = Ложь, для другого Спам = Истина. Таким образом, «Подозрительные слова» выбраны в качестве тестового атрибута для нового узла в левой ветви, как на рис. 18. На этом этапе подмножества данных в конце каждой ветви являются чистыми, поэтому алгоритм завершает работу и возвращает дерево решений, показанное на рис. 16.

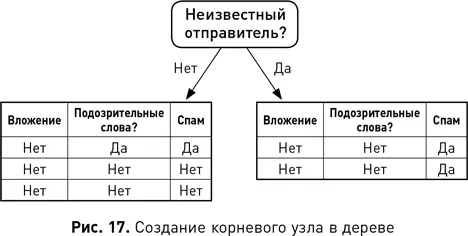
Одно из преимуществ деревьев решений заключается в том, что они понятны, притом с их помощью можно создавать очень точные модели. Например, модель «случайного леса» состоит из набора деревьев решений, где каждое дерево обучается случайной подвыборке обучающих данных, а прогноз, возвращаемый моделью для отдельного запроса, является прогнозом большинства деревьев в лесу. Хотя деревья решений хорошо работают с номинальными и порядковыми данными, они испытывают трудности с числовыми данными. В дереве решений существуют отдельные ветви, исходящие из каждого узла к каждому значению в области определения атрибута, проверяемого на узле. Числовые атрибуты, однако, могут иметь неограниченное число значений в своих областях определений, а это означает, что дереву потребуется бесконечное число ветвей. Одним из решений этой проблемы является преобразование числовых атрибутов в порядковые атрибуты, хотя для этого нужно определить соответствующие пороговые значения, что также может быть непросто.