Коллектив Авторов - Базы данных - конспект лекций

Здесь P = P < S 1∪ S 2> – условие, накладываемое на объединение двух схем исходных отношений-операндов. Именно по этому условию и происходит отбор кортежей из отношений r 1и r 2в результирующее отношение.

Следует отметить, что операция внутреннего соединения может применяться к отношениям с разными схемами отношений. Эти схемы могут быть любыми, но они ни в коем случае не должны пересекаться.

Кортежи исходных отношений-операндов, попавшие в результат операции внутреннего соединения, называются соединимыми кортежами.

Для наглядного иллюстрирования работы операции внутреннего соединения, приведем следующий пример.

Пусть нам даны два отношения r 1( S 1) и r 2( S 2) с различными схемами отношения:

r 1( S 1):

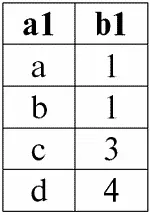
r 2( S 2):

Следующая таблица даст результат применения операции внутреннего соединения по условию P = (b1 = b2).

r 1( S 1) × P r 2( S 2):

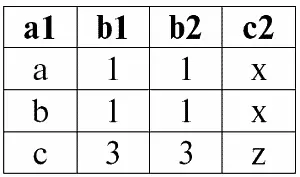
Итак, мы видим, что действительно «слипание» двух таблиц, представляющих отношения, произошло именно по тем кортежам, в которых выполняется условие операции внутреннего соединения P = (b1 = b2).

Теперь на основании уже введенной операции внутреннего соединения мы можем ввести операцию левого внешнего соединенияи правого внешнего соединения. Поясним.

Результатом операции левое внешнее соединение является результат внутреннего соединения, пополненный несоединимыми кортежами левого исходного отношения-операнда. Аналогично результат операции правого внешнего соединения определяется как результат операции внутреннего соединения, пополненный несоединимыми кортежами стоящего справа исходного отношения-операнда.

Вопрос, чем же пополняются результирующие отношения операций левого и правого внешнего соединения, вполне ожидаем. Кортежи одного отношения-операнда дополняются на схеме другого отношения-операнда Null-значениями.

Стоит заметить, что введенные таким образом операции левого и правого внешнего соединения являются производными операциями от операции внутреннего соединения.

Чтобы записать общие формулы для операций левого и правого внешнего соединений, проведем некоторые дополнительные построения.

Пусть нам даны два отношения r 1( S 1) и r 2( S 2) с различными схемами отношений S 1и S 2, не пересекающимися друг с другом.

Так как мы уже оговаривали, что операции левого и правого внутреннего соединения являются производными, то мы можем получить следующие вспомогательные формулы для определения операции левого внешнего соединения:

1) r 3( S 2 ∪ S 1) ≔ r 1( S 1) × P r 2( S 2) ;

r 3( S 2 ∪ S 1) — это просто результат внутреннего соединения отношений r 1( S 1) и r 2( S 2) . Левое внешнее соединение является производной операцией именно от операции внутреннего соединения, поэтому мы и начинаем наши построения с нее;

2) r 4( S 1) ≔ r 3( S 2 ∪ S 1) [ S 1] ;

Таким образом, с помощью унарной операции проекции, мы выделили все соединимые кортежи левого исходного отношения-операнда r 1( S 1) . Результат обозначили r 4( S 1) для удобства применения;

3) r 5( S 1) ≔ r 1( S 1) \ r 4( S 1) ;

Здесь r 1( S 1) — все кортежи левого исходного отношения-операнда, а r 4( S 1) – его же кортежи, только соединимые. Таким образом, при помощи бинарной операции разности, в отношении r 5( S 1) у нас получились все несоединимые кортежи левого отношения-операнда;

4) r 6( S 2)≔ {∅( S 2)};

{∅( S 2)} — это новое отношение со схемой ( S 2) , содержащее всего один кортеж, причем составленный из Null-значений. Для удобства мы обозначили это отношение r 6( S 2);

5) r 7( S 2 ∪ S 1) ≔ r 5( S 1) × r 6( S 2) ;