Коллектив Авторов - Базы данных - конспект лекций

Итак, рассмотрим операцию естественного соединения. Следует сразу заметить, что операндами этого действия могут являться отношения с разными схемами в отличие от трех бинарных операций объединения, пересечения и переименования.

Если рассмотреть два отношения с различными схемами отношений r 1( S 1) и r 2( S 2 ), то их естественным соединениембудет новое отношение r 3( S 3), которое будет состоять только из тех кортежей операндов, которые совпадают на пересечении схем отношений. Соответственно, схема нового отношения будет больше любой из схем отношений исходных, так как является их соединением, «склеиванием». Кстати, кортежи, одинаковые в двух отношениях-операндах, по которым и происходит это «склеивание», называются соединимыми.

Запишем определение операции естественного соединения на языке формул систем управления базами данных:

r 3( S 3) = r 1( S 1) × r 2( S 2) = { t ( S 1∪ S 2) | t [ S 1] ∈ r 1 & t ( S 2) ∈ r 2};

Рассмотрим пример, хорошо иллюстрирующий работу естественного соединения, его «склеивание». Пусть дано два отношения r 1( S 1) и r 2( S 2), в табличной форме представления соответственно равные:

r 1( S 1):

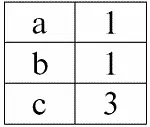
r 2( S 2):

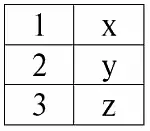
Мы видим, что у этих отношений присутствуют кортежи, совпадающие при пересечении схем S 1и S 2отношений. Перечислим их:

1) кортеж {a, 1} отношения r 1( S 1) совпадает с кортежем {1, x} отношения r 2( S 2);

2) кортеж {b, 1} из r 1( S 1) также совпадает с кортежем {1, x} из r 2( S 2);

3) кортеж {c, 3} совпадает с кортежем {3, z}.

Значит, при естественном соединении новое отношение r 3( S 3) получается «склеиванием» именно на этих кортежах. Таким образом, r 3( S 3) в табличном представлении будет выглядеть следующим образом:

r 3( S 3) = r 1( S 1) × r 2( S 2):

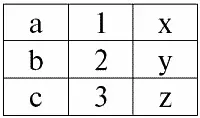
Получается по определению: схема S 3не совпадает ни со схемой S 1, ни со схемой S 2, мы «склеили» две исходные схемы по пересекающимся кортежам, чтобы получить их естественное соединение.

Покажем схематично, как происходит соединение кортежей при применении операции естественного соединения.

Пусть отношение r 1имеет условный вид:

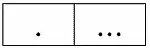
А отношение r 2– вид:

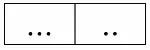
Тогда их естественное соединение будет выглядеть следующим образом:

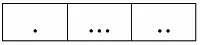
Видим, что «склеивание» отношений-операндов происходит по той самой схеме, что мы приводили ранее, рассматривая пример.

Операция декартового соединенияявляется частным случаем операции естественного соединения. Если конкретнее, то, рассматривая действие операции декартового произведения на отношения, мы заведомо оговариваем, что в этом случае может идти речь только о непересекающихся схемах отношений. В результате применения обеих операций получаются отношения со схемами, равными объединению схем отношений-операндов, только в декартово произведение двух отношений попадают всевозможные пары их кортежей, так как схемы операндов ни в коем случае не должны пересекаться.

Таким образом, исходя из всего вышесказанного запишем математическую формулу для операции декартового произведения:

r 4( S 4) = r 1( S1 ) × r 2( S 2) = { t ( S 1 ∪ S 2) | t [ S 1] ∈ r 1& t ( S 2) ∈ r 2}, S 1∩ S 2= ∅;

Теперь рассмотрим пример, чтобы показать, какой вид будет иметь результирующая схема отношения, при применении операции декартового произведения.