Коллектив Авторов - Базы данных - конспект лекций

Таким образом, пересечение двух отношений – это:

r 3( S ) = r 1( S ) ∪ r 2( S ) = { t ( S ) | t ∈ r 1∪ t ∈ r 2} ;

Для наглядности, приведем пример в терминах таблиц:

Пусть даны два отношения:

r 1( S ):

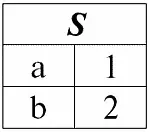
r 2( S ):

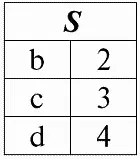
Мы видим, что схемы первого и второго отношений одинаковы, только имеют различной количество кортежей. Объединением этих двух отношений будет отношение r 3( S ) , которому будет соответствовать следующая таблица:

r3 ( S ) = r 1( S ) ∪ r 2( S ):

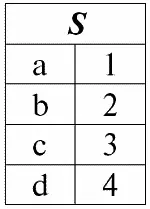
Итак, схема отношения S не изменилась, только выросло количество кортежей.

2. Перейдем к рассмотрению следующей бинарной операции – операции пересечениядвух отношений. Как мы знаем еще из школьной геометрии, в результирующее отношение войдут только те кортежи исходных отношений, которые присутствуют одновременно в обоих отношениях r 1( S ) и r 2( S ) (снова обращаем внимание на одинаковую схему отношения).

Операция пересечения двух отношений будет выглядеть следующим образом:

r 4( S ) = r 1( S ) ∩ r 2( S ) = { t ( S ) | t ∈ r 1& t ∈ r 2};

И снова рассмотрим действие этой операции над отношениями, представленными в виде таблиц:

r 1( S ):

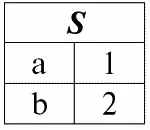
r 2( S ):

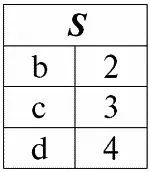
Согласно определению операции пересечением отношений r 1( S ) и r 2( S ) будет новое отношение r 4( S ) , табличное представление которого будет выглядеть следующим образом:

r 4( S ) = r 1( S ) ∩ r 2( S ):

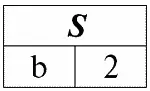
Действительно, если посмотреть на кортежи первого и второго исходного отношений, общий среди них только один: {b, 2}. Он и стал единственным кортежем нового отношения r 4( S ) .

3. Операция разностидвух отношений определяется аналогичным с предыдущими операциями образом. Отношения-операнды, так же, как и в предыдущих операциях, должны иметь одинаковые схемы отношения, тогда в результирующее отношение войдут все те кортежи первого отношения, которых нет во втором, т. е.:

r 5(S) = r 1(S) \ r 2(S) = {t(S) | t ∈ r 1& t ∉ r 2};

Уже хорошо знакомые нам отношения r 1( S ) и r 2( S ) , в табличном представлении выглядящие следующим образом:

r 1( S ):

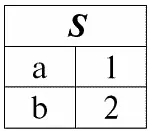
r 2( S ):

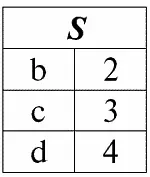
Мы рассмотрим как операнды в операции пересечения двух отношений. Тогда, следуя данному определению, результирующее отношение r5 ( S ) будет выглядеть следующим образом:

r 5( S ) = r 1( S ) \ r 2( S ):

Рассмотренные бинарные операции являются базовыми, на них основываются другие операции, более сложные.

Операция декартового произведения и операция естественного соединения являются бинарными операциями типа произведения и основываются на операции объединения двух отношений, которую мы рассматривали ранее.

Хотя действие операции декартова произведения многим может показаться знакомым, начнем мы все-таки с операции естественного произведения, так как она является более общим случаем, нежели первая операция.