Коллектив Авторов - Базы данных - конспект лекций

Сравним приведенные ранее примеры для операций естественного и внутреннего соединений.

Пусть нам даны два отношения r 1( S 1) и r 2( S 2) которые будут выступать в качестве операндов. Они равны:

r 1( S 1):

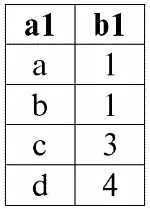
r 2( S 2):

Как мы уже получали ранее, результатом операции естественного соединения этих отношений будет являться таблица следующего вида:

r 3( S 3) ≔ r 1( S 1) × r 2( S 2):

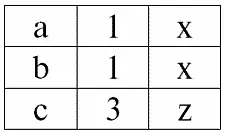
А результатом внутреннего соединения этих же отношений r 1( S 1) и r 2( S 2) по условию P = (b1 = b2) будет следующая таблица:

r 4( S 4) ≔ r 1( S 1) × P r 2( S 2):

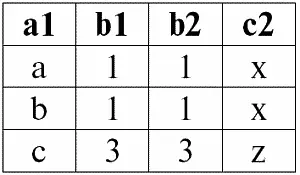
Сравним эти два результата, получившиеся новые отношения r 3( S 3) и r 4( S 4).

Ясно, что операция естественного соединения выражается через операцию внутреннего соединения, но, что главное, с условием соединения специального вида.

Запишем математическую формулу, описывающую действие операции естественного соединения как производную операции внутреннего соединения.

r 1( S 1) × r 2( S 2) = { ρ < ϕ 1> r 1× E ρ < ϕ 2> r 2}[ S 1 ∪ S 2],

где E — условие соединимостикортежей;

E = ∀ a ∈ S 1∩ S 2[ IsNull ( b 1) & IsNull (2) ∪ b 1 = b 2];

b 1= ϕ 1( name ( a )) , b 2= ϕ 2( name ( a ));

Здесь одна из функций переименования ϕ 1является тождественной, а другая функция переименования (а именно – ϕ 2) переименовывает атрибуты, на которых наши схемы пересекаются.

Условие соединимости E для кортежей записывается в общем виде с учетом возможных появлений Null-значений, ведь операция внутреннего соединения (как уже было сказано выше) является производной операцией от операции декартового произведения двух отношений и унарной операции выборки.

Покажем, как можно использовать рассмотренные ранее выражения и операции реляционной алгебры в практической эксплуатации различных баз данных.

Пусть для примера в нашем распоряжении имеется фрагмент какой-то коммерческой базы данных:

Поставщики ( Код поставщика , Имя поставщика, Город поставщика);

Инструменты ( Код инструмента , Имя инструмента, …);

Поставки ( Код поставщика , Код детали );

Подчеркнутые имена атрибутов [1]являются ключевыми (т. е. идентификационными) атрибутами, причем каждый в своем отношении.

Предположим, что к нам, как разработчикам этой базы данных и хранителям информации по этому вопросу, поступил заказ получить наименования поставщиков (Имя Поставщика) и место их расположения (Город Поставщика) в случае, когда эти поставщики не поставляют каких-либо инструментов с родовым именем «Плоскогубцы».

Чтобы в нашей, возможно, весьма обширной, базе данных определить всех поставщиков, отвечающих этому требованию, запишем несколько выражений реляционной алгебры.

1. образуем естественное соединение отношений «Поставщики» и «Поставки» для того, чтобы сопоставить с каждым поставщиком коды поставляемых им деталей. Новое отношение – результат применения операции естественного соединения – для удобства дальнейшего применения обозначим через r 1.

Поставщики × Поставки ≔ r 1(Код поставщика, Имя поставщика, Город поставщика, Код поставщика, Код инструмента);

В скобках мы перечислили все атрибуты отношений, участвующих в этой операции естественного соединения. Мы видим, что атрибут «Код поставщика» дублируется, но в итоговой записи операции каждое имя атрибута должно присутствовать только один раз, т. е.:

Поставщики × Поставки ≔ r 1(Код поставщика, Имя поставщика, Город поставщика, Код инструмента);