Коллектив Авторов - Базы данных - конспект лекций

Здесь мы взяли полученные в пункте три, несоединимые кортежи левого отношения-операнда ( r 5( S 1)) и дополнили их на схеме второго отношения-операнда S 2Null-значениями, т. е. декартово умножили отношение, состоящее из этих самых несоединимых кортежей на отношение r 6( S 2) , определенное в пункте четыре;

6) r 1( S1 ) →× Pr 2( S 2) ≔ ( r 1× P r 2) ∪ r 7( S 2∪ S 1);

Это и есть левое внешнее соединение, полученное, как можно видеть, объединением декартового произведения исходных отношений-операндов r 1и r 2и отношения r 7( S 2 ∪ S 1), определенного в пункте пятом.

Теперь у нас имеются все необходимые выкладки для определения не только операции левого внешнего соединения, но по аналогии и для определения операции правого внешнего соединения. Итак:

1) операция левого внешнего соединенияв строгом формулярном виде выглядит следующим образом:

r 1( S 1 ) →× P r 2( S 2) ≔ ( r 1× P r 2) ∪ [( r 1\ ( r 1× P r 2) [ S 1]) × {∅( S 2)}];

2) операция правого внешнего соединенияопределяется подобным образом операции левого внешнего соединения и имеет следующий вид:

r 1( S 1 ) →× P r 2( S 2) ≔ ( r 1× P r 2) ∪ [( r 2\ ( r 1× P r 2) [ S 2]) × {∅( S 1)}];

Эти две производные операции имеют всего два свойства, достойные упоминания.

1. Свойство коммутативности:

1) для операции левого внешнего соединения:

r 1( S 1) →× P r 2( S 2) ≠ r 2( S 2) →× P r 1( S 1);

2) для операции правого внешнего соединения:

r 1( S 1) ←× P r 2( S 2) ≠ r 2( S 2) ←× P r 1( S 1)

Итак, мы видим, что свойство коммутативности не выполняется для этих операций в общем виде, но при этом операции левого и правого внешнего соединения взаимно обратны друг другу, т. е. выполняется:

1) для операции левого внешнего соединения:

r 1( S 1) →× P r 2( S 2) = r 2( S 2) →× P r 1( S 1) ;

2) для операции правого внешнего соединения:

r 1( S 1) ←× P r 2( S 2) = r 2( S 2) ←× P r 1( S 1) .

2. Основным свойством операций левого и правого внешнего соединения является то, что они позволяют восстановитьисходное отношение-операнд по конечному результату той или иной операции соединения, т. е. выполняются:

1) для операции левого внешнего соединения:

r 1( S1 ) = ( r 1→× P r 2) [ S 1];

2) для операции правого внешнего соединения:

r 2( S 2) = ( r 1←× P r 2) [ S 2] .

Таким образом, мы видим, что первое исходное отношение-операнд можно восстановить из результата операции левого правого соединения, а если конкретнее, то применением к результату этого соединения ( r 1× r 2) унарной операции проекции на схему S 1, [ S 1].

И аналогично второе исходное отношение-операнд можно восстановить применением к результату операции правого внешнего соединения ( r 1× r 2) унарной операции проекции на схему отношения S 2.

Приведем пример для более подробного рассмотрения работы операций левого и правого внешних соединений. Введем уже знакомые нам отношения r 1( S 1) и r 2( S 2) с различными схемами отношения:

r 1( S 1):

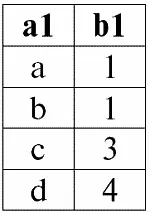
r 2( S 2):

Несоединимый кортеж левого отношения-операнда r 2( S 2) – это кортеж {d, 4}. Следуя определению, именно им следует дополнить результат внутреннего соединения двух исходных отношений-операндов.

Условие внутреннего соединения отношений r 1( S 1) и r 2( S 2) также оставим прежнее: P = (b1 = b2). Тогда результатом операции левого внешнего соединениябудет следующая таблица:

r 1( S 1) →× P r 2( S 2):

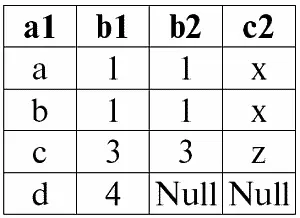
Действительно, как мы можем видеть, в результате воздействия операции левого внешнего соединения, произошло пополнение результата операции внутреннего соединения несоединимыми кортежами левого, т. е. в нашем случае первого отношения-операнда. Пополнение кортежа на схеме второго (правого) исходного отношения-операнда по определению произошло при помощи Null-значений.