Елена Чиркова - Как оценить бизнес по аналогии - Пособие по использованию сравнительных рыночных коэффициентов

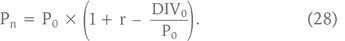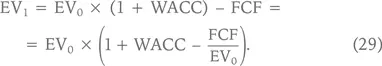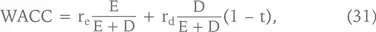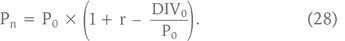
Аналогичным образом можно рассчитать и будущую стоимость компании – EV. Существуют два метода расчета будущей величины EV. Первый метод – прямой: по той же формуле, по которой рассчитывалась будущая стоимость акции. Отличие состоит в том, что при определении стоимости бизнеса (EV) доходность, требуемая инвесторами на вложения в акции, будет заменена в этой формуле на WACC – средневзвешенную стоимость капитала или средневзвешенную доходность для всех сторон, финансирующих компанию, а дивиденды, или денежные потоки акционеров, будут заменены на доходы всех провайдеров капитала, т. е. на свободный денежный поток, попавший в распоряжение акционеров и кредиторов (назовем его в нижеследующей формуле для краткости FCF (денежный поток акционеров и кредиторов – free cash flow)).

Тогда мы получим «аналог» формулы (27) для стоимости бизнеса:

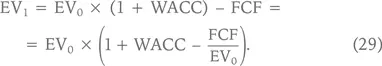
По аналогии с тем, как DIVt/Pt – 1 называют dividend yield, FCFt/EVt – 1 называют FCF yield, что можно попытаться перевести весьма громоздкой фразой «доходность бизнеса по денежному потоку (акционеров и кредиторов)».

Для случая, когда WACC = const и FCF yield = const, формула EVn выглядит следующим образом:

EVn = EV0 × (1 + WACC) – FCF yieldn. (30)

Напомним, что WACC рассчитывается по формуле:

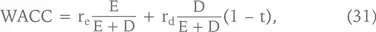
где E [69] Не путать с символом E, которым обозначается чистая прибыль, в данном случае E – это рыночная капитализация, которую мы ранее обозначали МС. Формула приводится в таком виде, поскольку именно так она выглядит во многих учебниках по финансам. – рыночная стоимость акционерного капитала;

re – требуемая доходность на акционерный капитал;

D – рыночная стоимость долга;

rd – процентная ставка по долгу;

t – ставка налога на прибыль;

rd × (1 – t) – посленалоговая (after tax) процентная ставка.

Второй метод – косвенный: тот же результат можно получить, прибавив к будущей рыночной капитализации будущий чистый долг, который, в свою очередь, будет рассчитываться из текущего чистого долга с учетом его изменений (выплаты процентов и изменения основной суммы долга) за требуемый период.

Рассмотрим такие расчеты на примере. Предположим, что текущая рыночная капитализация компании составляет $120, чистый долг – $80, стоимость привлечения акционерного капитала – 12 %, а посленалоговая процентная ставка по кредитам – 6 %. В году 1 свободный денежный поток компании составит $26, дивиденды – $10, а весь излишек за вычетом процентов и дивидендов пойдет на уменьшение основной суммы долга. В году 2 свободный денежный поток составит $10, компания выплатит дивиденды в размере $8, а недостающие средства для выплаты процентов будут финансироваться за счет нового долга. Нужно найти стоимость акций и стоимость бизнеса в году 2.

Сначала разберемся с будущей стоимостью акций. Согласно формуле (27), стоимость акций в году 1 будет равна: P1 = 120 × (1 + 12 %) – 10 = $124,4, а в году 2: Р2 = 124,4 × (1 + 12 %) – 8 = $131,3. Теперь рассчитаем стоимость бизнеса в году 1. Согласно формуле (31) средневзвешенная стоимость капитала в году 1 равна: WACC1 = 12 % × 120/(120 + 80) + 6 % × 80/(120 + 80) = 9,6 %. Тогда, по формуле (29), т. е. по расчетам прямым методом, стоимость бизнеса в году 1 будет равна: EV1 = (120 + 80) × (1 + 9,6 %) – 26 = $193,2.

Процентные выплаты в году 1 составят $80 × 6 % = $4,8. Следовательно, чистый долг уменьшится на 26 – 10 – 4,8 = $11,2 и составит $68,8. В соответствии с косвенным методом: EV1 = 124,4 + 68,8 = $193,2, что в точности совпадает с расчетом прямым методом.

Аналогично для года 2: WACC2 = 12 % × 124,4/193,2 + 6 % × 68,8/193,2 = 9,86 %. В году 2 компания выплатит проценты в размере $68,8 × 6 % = $4,13. Долг увеличится на 8 + 4,13 – 10 = $2,13 и составит $70,93. Тогда, используя прямой метод, получим: EV2 = 193,2 × (1 + 9,86 %) – 10 = $202,24 [70] Обращаю внимание читателя на то, что $10 вычитаются не потому, что компания заработала эти $10, а потому, что отток из компании составил $10. Из этой суммы $8 полагается акционерам в виде дивидендов, а $4,13 – кредиторам в виде процентов, но у последних было занято $2,13, поэтому они фактически получили только $2. , а косвенный метод: EV2 = 131,3 + 70,93 = $202,23. Таким образом, результаты практически совпали (разница в одну сотую – ошибка округления).

Итак, мы научились рассчитывать мультипликаторы на основе форвардных цен, но в чем смысл этой трудоемкой работы? [71] Кстати, работа эта еще более трудоемкая, чем кажется на первый взгляд, поскольку, производя сравнительную оценку при помощи таких мультипликаторов, мы должны будем потом пересчитать из нее текущую оценку. Как вы догадались, далее будет дан ответ на контрольный вопрос 13. Если посмотреть внимательно на суть мультипликаторов, в которых корректировке на будущие изменения подвергается лишь знаменатель (прибыль, выручка и т. п.), о них шла речь в предыдущих параграфах, то они позволяют учитывать разницу в темпах роста между оцениваемой компанией и аналогом, однако игнорируют источник этого роста. Таким образом, они не учитывают, каким является рост: экстенсивным, т. е. вызванным более высокой долей свободного денежного потока, которая направлена на реинвестирование, или интенсивным – вызванным более высокой доходностью вложений, измеряемой как ROIC (return on invested capital) или ROE (return on equity). Как мы помним, темпы роста компании и доходность капитала связаны простой формулой (20): g = ROE × b, где b – доля реинвестированной прибыли. В табл. 8 показана зависимость темпов роста прибыли от темпов реинвестирования для разной доходности акционерного капитала. Например, при доходности 10 % в год и реинвестировании 25 % чистой прибыли темпы роста чистой прибыли составят 3 %, а при реинвестировании 75 % – около 8 %.