Елена Чиркова - Как оценить бизнес по аналогии - Пособие по использованию сравнительных рыночных коэффициентов

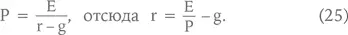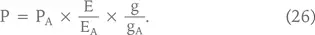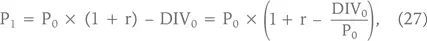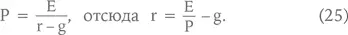
Рассчитав по этой формуле rА для компании-аналога, применим такой же rБ (равный rА) для оцениваемой компании и найдем ее стоимость по формуле Гордона. Затем найдем стоимость оцениваемой компании по мультипликатору, т. е. исходя из предположения о том, что (РА/ЕА)/gА = (РБ/ЕБ)/gБ:

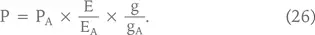
Уже на уровне чистой математики можно заметить, что результаты расчетов по формуле (26) только случайно могут совпадать с результатами дисконтирования. Например, согласно формуле Гордона денежный поток в размере $1, растущий темпами 5 % в год и дисконтируемый под 20 %, дает капитализацию 1/(20 % – 5 %) = 1/15 % = $6,66. Если же темпы роста денежного потока возрастают в два раза (с 5 до 10 %), дисконтирование под 20 % приводит к капитализации 1/(20 % – 10 %) = 1/10 = $10, что в 1,5, а не в 2 раза (как это предполагается при применении показателя (P/Е)/g) выше, чем стоимость потока, растущего на 5 % в год.

Из вышеприведенного примера можно видеть, что показатель (Р/Е)/g завышает стоимость акций оцениваемой компании, если аналог растет более медленными темпами. Еще большее искажение в оценке стоимости при использовании (Р/Е)/g возникнет, если оцениваемая компания будет расти более высокими темпами только ограниченный период времени, а затем ее темпы роста снизятся.

Однако не будем списывать этот мультипликатор со счетов. Во-первых, он прижился. Например, финансовый портал Yahoo! где можно найти обширную информацию по любой котируемой компании, включил его в стандартное описание наряду с P/S и P/E, а других мультипликаторов там нет. Кроме того, как я показываю в разделе «Абсолютное и относительное» главы 12, сходный с ним мультипликатор (DIV/P+g)/(P/E) используется выдающимися инвесторами для грубой прикидки переоцененности или недооцененности акций.

При прочих равных условиях у какой компании показатель (P/Е)/g будет выше?

A. У компании с более высокими или более низкими темпами роста.

Б. У высоко- или низкорисковой компании.

B. У компании с большей или меньшей доходностью акционерного капитала.

Г. У компании, которая реинвестирует большую или меньшую долю прибыли.

До сих пор мы конструировали мультипликаторы, основанные на будущих показателях компании, оперируя лишь знаменателем мультипликатора, между тем в числителе стояла текущая цена акций. А теперь я задам очень сложный вопрос, пожалуй, самый сложный в данной книге.

В чем недостатки подхода, при котором по «показателям будущего» мы корректируем только знаменатель мультипликатора? В каких случаях он менее всего применим? Попытайтесь придумать пример.

Такой пример постаралась придумать и я, но о нем речь пойдет чуть позже, а пока мы займемся тем, что введем новый вид мультипликаторов, у которых не только знаменатель, но и числитель являются оценками будущего. Сначала аналитики ввели ожидаемые оценки в числитель мультипликаторов вида «EV/…». Показатель EV, представляющий собой сумму цен акций и чистого долга, стали заменять на сумму вида MC0 + NDt, т. е. на сумму текущей капитализации и будущего чистого долга. Такая сумма является чисто умозрительной конструкцией, однако поправка на будущий долг позволила сделать более корректным сравнение компаний, у которых изменение чистого долга в прогнозном периоде будет демонстрировать разную динамику.

Затем появились мультипликаторы, в числителе которых использовались и будущие цены акций, поэтому мы будем называть их «мультипликаторами на основе форвардных цен» (forward priced, или forward looking multiples). Числитель таких мультипликаторов имеет вид: MCt + NDt.

Мы можем рассчитать цену акции в будущем периоде по следующей формуле:

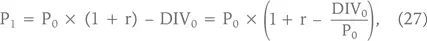
где r – как всегда, доходность, требуемая инвесторами на вложения в данную акцию, DIV – дивиденды, а DIV0/P0 – «доходность акции по дивидендам», или «дивидендная доходность» (dividend yield). Если r1 = r2 =… = rn и DIV0/P0 = DIV1/P1 =… = DIVn/Pn; то [68] В общем виде в данной формуле под показателем «дивиденды» (DIV) подразумеваются все выплаты акционерам, которые могут включать также доходы от продажи акций компании, если она выкупает свои акции на баланс, или расходы на покупку акций новой эмиссии (в этом случае – с обратным знаком), но поскольку по причинам, изложенным в разд. 3.1, нас интересует оценка одной акции, от этих эффектов мы абстрагируемся.