Тим Филлипс - Управление на основе данных. Как интерпретировать цифры и принимать качественные решения в бизнесе

Ежеквартальную публикацию показателя ВВП всегда ожидают с нетерпением, как и статистику по уровню безработицы, кредитованию или инвестициям. Единственная проблема заключается в том, что этот показатель будет заведомо неправильным.

Это можно утверждать с уверенностью, потому что вся официальная статистика впоследствии уточняется. Показатель ВВП уточняется в следующем квартале, году и так далее. Специалисты Организации экономического сотрудничества и развития (ОЭСР), международной экономической организации развитых стран, проанализировали индикаторы ВВП, которые публиковались в последнее время, и пришли к заключению, что, как правило, через три года средняя коррекция по всем странам составила 0,2 процентных пункта. Мелочь? Но эта мелочь составляет среднюю погрешность измерения в $200 млрд.

Так происходит не потому, что специалисты по статистике не справляются с работой. Показатель ВВП, как и уровня безработицы, создания новых рабочих мест или годового оборота вашей компании, складывается из многих цифр, которые измеряются отдельно. Каждый из этих отдельных показателей может иметь погрешность, и эти погрешности суммируются.

Максимально возможная точность статистических данных чрезвычайно важна. Однако имеет значение еще один момент – фактор времени: нам нужно хотя бы примерно понимать, в какой точке мы сейчас находимся. Если бы мы три года ждали точного показателя ВВП, правительство и бизнес просто не смогли бы принимать решения. Это компромиссный вариант.

Аналогичным образом вам требуются максимально точные данные, которые вы можете получить в нужное время. Получить их без ошибки практически невозможно, поэтому вам предстоит решить, стоит ли ждать, пока не станут доступны более качественные данные, или потратить время на проведение более точных расчетов. Обычно примерного грубого расчета может оказаться вполне достаточно, если всем известен предел погрешности.

Итак, перед нами две проблемы: одно дело, если вы готовите отчет, а другое – если принимаете решение, опираясь на данные. Мы склонны переоценивать надежность измеряемых данных, а также находить закономерности и тренды в том, что может оказаться лишь погрешностью в вычислениях.

Простая практика – не преувеличивать важность точности при составлении таблиц и диаграмм. Нередко мы поддаемся этому, так как в Excel высчитываются проценты с точностью до двух знаков после запятой. Предположим, вы проводите опрос коллег, где лучше организовать рождественскую вечеринку, и получаете 23 ответа:

Согласно моей программе по созданию таблиц, это означает:

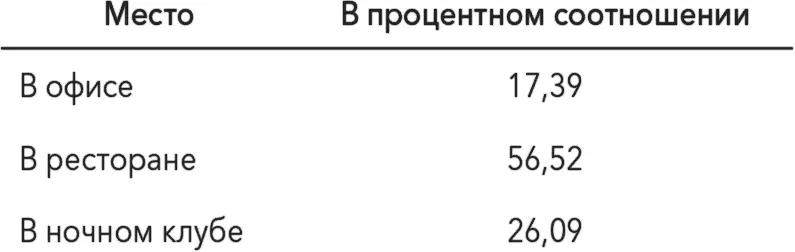
Но в чем суть десятичных значений? Вполне достаточно: 17 %, 57 % и 26 %. Хотя фактически цифры 4, 13 и 6 и так сообщают вам все, что нужно: большинство ваших коллег предпочитают пойти в ресторан. К показателям, которые получаются с помощью измерения, тоже следует относиться осмотрительно. Например, показатель вашей массы тела слегка изменяется в течение дня, поэтому не нужно бить тревогу, если сегодня после плотного ужина ваш вес на 0,5 кг больше, чем вчера утром. Это может быть как изменением массы тела, так и погрешностью вычислений. Возможно, в некоторых случаях оптимальным вариантом будет брать среднее арифметическое после нескольких измерений, но опять-таки не перестарайтесь с точностью.

Анализируя результаты исследований, подойдите к вопросу с другой стороны. Публикуемая статистика всегда должна приводиться с возможной погрешностью вычислений. В качественных таблицах и диаграммах отражается погрешность вычислений на коэффициент достоверности (90 % или 95 % – наиболее характерные показатели). Погрешность плюс-минус 2 % на коэффициент достоверности 90 % означает, что, если провести измерения 100 раз, 90 раз полученный результат не будет отклоняться от опубликованного показателя больше чем на 2 % в любую сторону.

Это чрезвычайно важная информация, если вы опираетесь на опубликованную статистику при принятии решений. Если статистические данные вам предоставляет какая-то компания, попросите ее отмечать эти интервалы в виде планок погрешности.

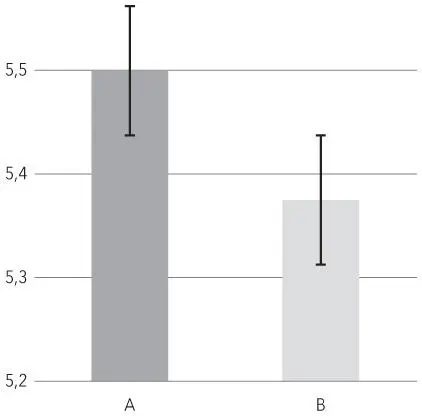
Столбец справа кажется меньше левого, но при этом планки погрешности пересекаются. Сложно сказать, означает ли это, что статистические данные, которые мы измеряли, разнятся в двух группах, учитывая наш доверительный интервал (если планки погрешности не пересекаются, тогда в этом можно быть уверенными).