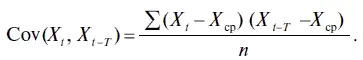Владимир Брюков - Как предсказать курс доллара. Эффективные методы прогнозирования с использованием Excel и EViews

Оптимальными для валютной торговли являются цены покупки или продажи, установленные в диапазоне от 60 до 90 % уровня надежности, поскольку при дальнейшем снижении уровня надежности у инвестора начинает резко падать вероятность удачной сделки, а при превышении 90 %-ного уровня надежности значительно вырастает риск упущенной прибыли, в то время как вероятность удачной сделки повышается не столь существенно.

Теперь проверим, насколько эффективным могло быть использование рассчитанных нами цен покупки и продажи в ходе торгов на валютном рынке в августе 2010 г. Поскольку до 10 августа в динамике курса доллара преобладал падающий тренд (рис. 7.1), то первым в торгах смог поучаствовать инвестор (сделка была совершена 4 августа), установивший цену покупки с 60 %-ным уровнем надежности. Однако начиная с 11 августа американская валюта начала устойчиво расти, поэтому на рынок стали выходить игроки, планировавшие продать доллар. В результате 13 августа сделку совершил инвестор, установивший цену продажи с 60 %-ным уровнем надежности, 24 августа — инвестор, установивший цену продажи с 70 %-ным уровнем надежности, с 26 августа — инвестор, установивший цену продажи с 80 %-ным уровнем надежности. Вместе с тем инвестор, установивший цену продажи с 90 %-ным уровнем надежности, на рынок выйти не смог, поскольку курс доллара не вырос до этого уровня. Тем более не смогли участвовать в торгах (из-за отсутствия ожидаемого тренда) инвесторы, установившие цену покупки с 70 %-ным, 80 %-ным и 90 %-ным уровнями надежности.

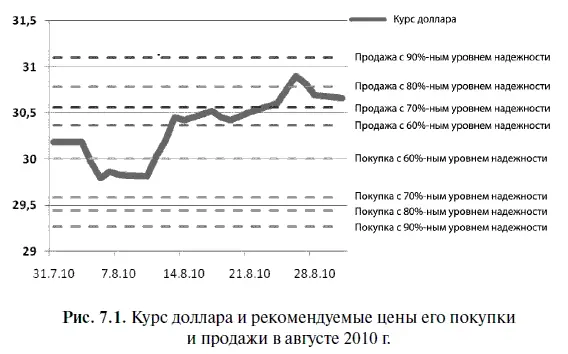
В таблице 7.5 представлены итоги валютных торгов за период с 1 августа по 31 августа 2010 г. для инвесторов, установивших цены покупки или продажи доллара с разными уровнями надежности. Судя по этой таблице, наиболее высокую курсовую доходность в размере 2,35 % по итогам августа получил инвестор, установивший цену продажи доллара с 80 %-ным уровнем надежности. На втором месте по этому показателю (с 2,32 %-ной доходностью) инвестор, установивший цену покупки с 60 %-ным уровнем надежности. Очевидно, что курсовая доходность у последнего инвестора была обеспечена за счет большего риска, однако поскольку тренд на рынке изменился в сторону роста, то этот риск оказался оправданным.

На третьем месте оказался инвестор, придерживавшийся консервативной стратегии «купил и держи», доходность которой в конце месяца составила 1,58 %. Кстати, фактическая вероятность удачной сделки для инвестора, всегда придерживавшегося этой стратегии, по нашим подсчетам, за период с октября 1998 г. по август 2010 г. равна 55,2 % (подсчет велся на конец каждого инвестиционного периода). Как видим, последняя цифра свидетельствует в пользу того, что американская валюта чаще растет, чем падает. Для справки заметим, что фактическая вероятность удачной сделки для инвестора, установившего цену покупки доллара с 60 %-ным уровнем надежности, за этот же период оказалась существенно выше — 73,2 %.

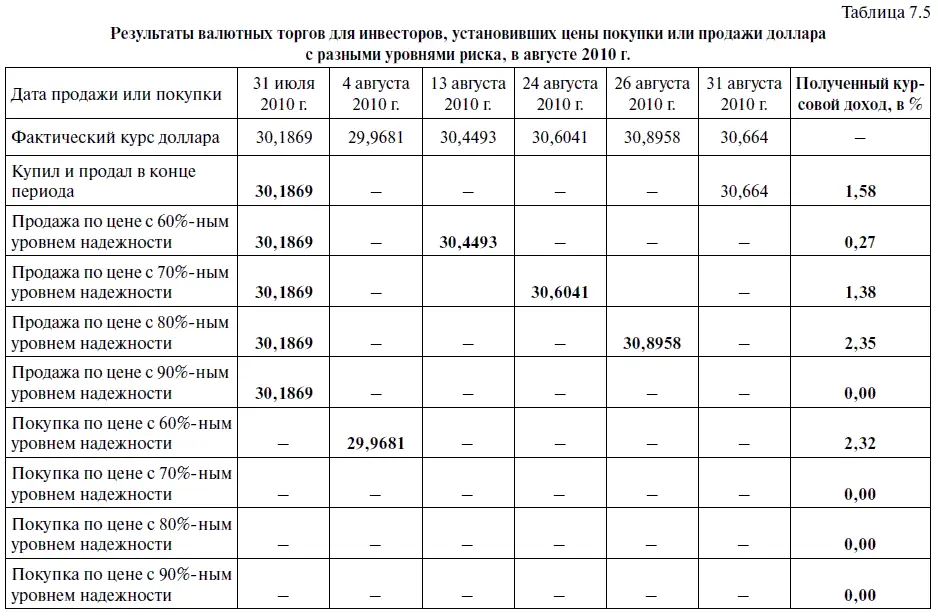
В большей части книги рассматривались статистические модели, делающие прогноз по курсу доллара с упреждением в один месяц, однако теперь перейдем к моделям, которые будут прогнозировать с упреждением в две недели, одну неделю и один день. Причем прогноз будет делаться не только по курсу доллара к рублю, но по и курсу евро к доллару. Нужно сразу отметить, что при переходе к прогнозированию с меньшим сроком упреждения точность наших моделей существенно повысится. И это вполне понятно с точки зрения здравого смысла, а с математической точки зрения объясняется следующим образом. Для оценки тесноты и направления связи между переменными одного временного ряда с определенным лагом используется автоковариация, которая находится по формуле (1.3)

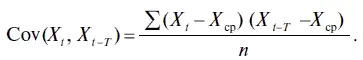
Однако, как в свое время писал специалист по теории вероятностей и случайным процессам А А. Свешников: «… при достаточно большом значении интервала времени T = t 1— t 2отклонение ординаты случайной функции от ее математического ожидания в момент времени t 2становится практически независимым от значения этого отклонения в момент времени t 1. В этом случае функция Cov, дающая значение корреляционного момента между Х ( t 1) и X ( t 2), при T → ∞ будет стремиться к нулю» [19] Свешников АЛ. Прикладные методы теории случайных функций. М.: Наука, 1968. С. 33. .