Владимир Брюков - Как предсказать курс доллара. Эффективные методы прогнозирования с использованием Excel и EViews

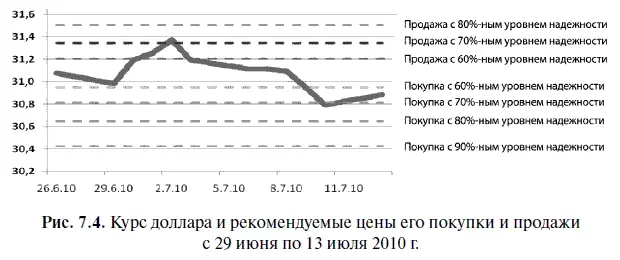
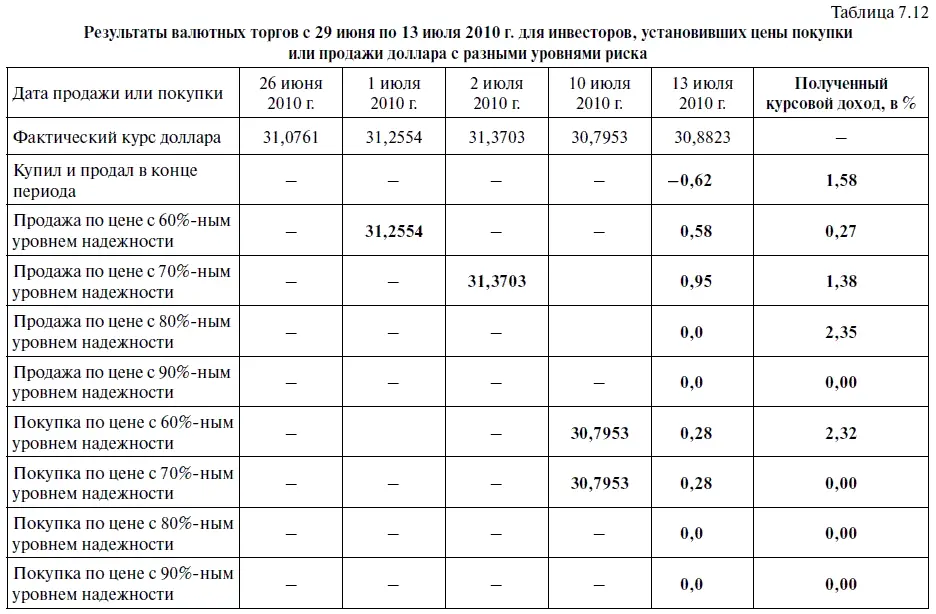
В таблице 7.12 представлены итоги валютных торгов за период с 29 июня по 13 июля 2010 г. для инвесторов, установивших цены покупки или продажи доллара с разными уровнями надежности. Судя по этой таблице, наиболее высокую курсовую доходность в размере 0,95 % по итогам двухнедельного инвестиционного периода получил инвестор, установивший цену продажи доллара с 70 %-ным уровнем надежности. На втором месте по этому показателю оказался инвестор, установивший цену продажи доллара с 60 %-ным уровнем надежности: доходность — 0,58 %. Третье место по доходности досталось инвесторам, установившим цену покупки доллара с 60 %-ным и 70 %-ным уровнями надежности, поскольку доходность у обоих оказалась равна 0,28 %. В то время как инвестор, придерживавшийся стратегии «купил и держи», в течение двух недель понес убытки в размере 0,62 %. При этом заметим, что фактическая вероятность удачной сделки для инвестора, придерживавшегося этой стратегии, по нашим подсчетам, за период с октября 1998 г. по июнь 2010 г. составила 52,0 % (из 306 сделок 152 были удачными, если вести подсчет доходности на конец каждого инвестиционного периода).

Сейчас рассмотрим, насколько эффективна для использования в валютных торгах статистическая модель, по которой можно делать прогноз по курсу доллара к рублю с упреждением в одну неделю. При этом на полном изложении процедуры построения такой прогностической модели особо останавливаться не будем, а расскажем о наиболее важных особенностях этой модели.

На основе базы данных по курсу доллара, взятых с интервалом в одну неделю (на конец периода) с 1 октября 1998 г. по 20 июля 2010 г., нами была построена прогностическая модель, по которой можно делать прогнозы с упреждением в одну неделю. Вывод данных по итогам решения уравнения регрессии можно увидеть в табл. 7.13.

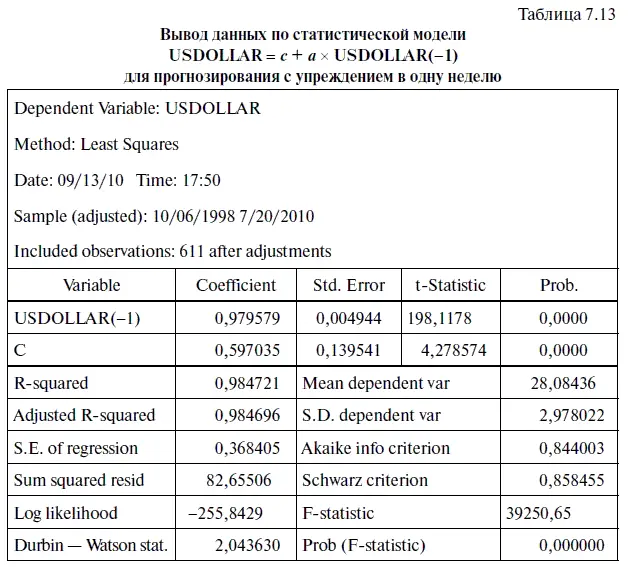
Подставив в USDOLLAR = с + а × USDOLLAR(-l) коэффициенты из табл. 7.13, получим следующую формулу:

USDOLLAR = 0,5970 + 0,9796 × USDOLLAR(-l), (7.4)

где USDOLLAR, USDOLLAR(-l) — переменные, обозначающие текущий курс доллара и курс доллара с лагом в одну неделю.

Интерпретация уравнения (7.4) следующая: в период с 1 октября 1998 г. по 20 июня 2010 г. рост на 1 руб. курса доллара с лагом в одну неделю в среднем приводил к повышению прогнозируемого курса доллара на 0,9796 руб. при исходном уровне курса доллара, равном 0,5970 руб.

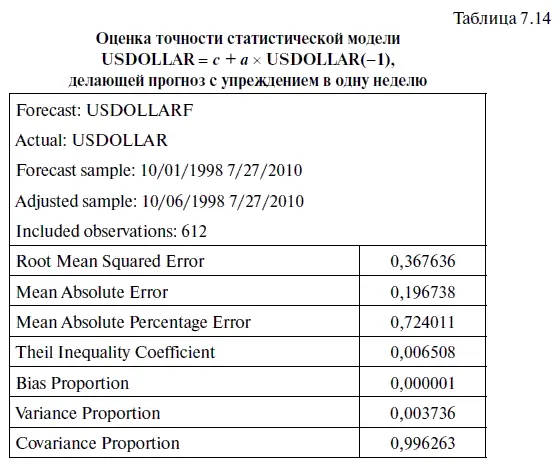
Теперь оценим точность полученной статистической модели (см. алгоритм действий № 8 «Как оценить точность статистической модели в EViews»), поместив результаты этой оценки в табл. 7.14. Судя по этой таблице, среднее отклонение по модулю курса доллара от его прогноза за весь период составило 19,7 коп., а среднее отклонение по модулю в процентах равняется 0,72 %. В то время как у модели USDOLLAR = с + а × USDOLLAR(-l) + b × USDOLLAR(-2), делающей прогнозы с упреждением в две недели, среднее отклонение по модулю курса доллара от его прогноза оказалось равно 28,9 коп., а среднее отклонение по модулю в процентах — 1,07 % (см. табл. 7.7).

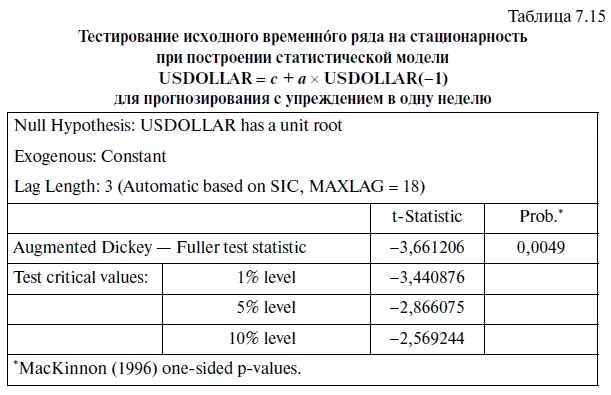
Поскольку модель, построенная с использованием исходного уровня временнбго ряда, оказалась стационарной, то в этом случае мы не стали переходить к логарифмическому временн о му ряду. О стационарности исходного временнбго ряда свидетельствуют итоги тестирования исходного временнбго ряда на стационарность с помощью расширенного теста Дикки — Фуллера (табл. 7.15). При этом уровень значимости (Prob. *) одностороннего t -критерия (t-Statistic) получился весьма близким к нулю, а потому нулевая гипотеза о нестационарности исходного временнбго ряда отвергается и принимается альтернативная гипотеза о его стационарности.

Для проверки качества этой статистической модели посмотрим, во-первых, как изменяется с увеличением лага автокорреляция и частная автокорреляция в остатках, во-вторых, насколько соответствуют фактические значения коррелограммы остатков их теоретическим значениям. Судя по рис. 7.5, по мере роста величины лага уровень автокорреляции постепенно снижается, асимптотически стремясь к нулю, а частная автокорреляция упала почти до нуля уже со второго лага. Если сравнить фактический уровень автокорреляции и частной автокорреляции (нижние вертикальные линии) с их теоретическими значениями (верхняя линия), то можно заметить, что они в основном совпадают. Вместе с тем следует отметить, что фактический уровень автокорреляции после пятого лага заметно ниже ее теоретического уровня, а фактический уровень частной автокорреляции после 10-го лага в некоторых случаях выше теоретического нулевого уровня.