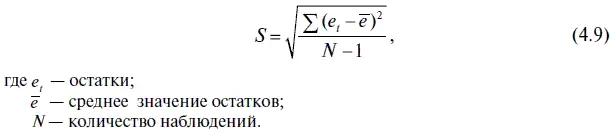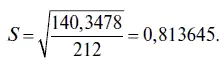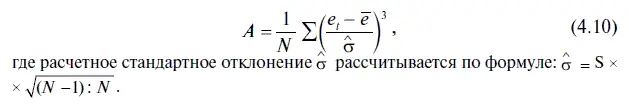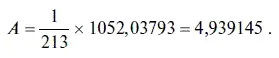4.3. Описательная статистика и тестирование остатков на нормальное распределение
Теперь нашей задачей является ответить на следующий важный вопрос: является ли распределение полученных остатков нормальным? При составлении интервальных прогнозов мы исходим из предположения, что распределение остатков носит нормальный характер, поэтому теперь должны проверить, насколько это утверждение соответствует истине.
Алгоритм действий № 10
Как в EViews получить описательную статистику остатков
Шаг 1. Установка необходимых опций
Чтобы узнать характер распределения остатков, необходимо в рабочем файле открыть файл RESID, а затем выбрать опции VIEW (CMOTpeTb)ZDESCRIPTIVE STATISTICS (описательная статистика)/ STATS TABLE (таблица со статистикой). В результате мы получили табл. 4.5 с описательной статистикой для остатков.
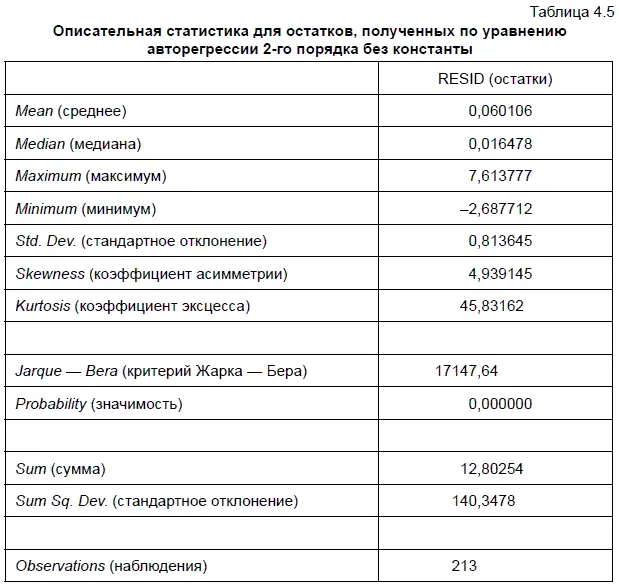
Шаг 2. Интерпретация результатов теста
Во-первых, если Probability (значимость) больше 0,05, то гипотеза о нормальном распределении остатков подтверждается. Поскольку в нашем случае Probability = 0, то гипотеза о нормальном распределении остатков отклоняется. Во-вторых, если коэффициент асимметрии (Skewness) больше нуля, то в остатках наблюдается правосторонняя асимметрия, а если меньше нуля — левосторонняя асимметрия. Судя по табл. 4.5, в этом случае в распределении остатков наблюдается правосторонняя асимметрия. Если коэффициент эксцесса (Kurtosis) больше 3, то наблюдается островершинное распределение, а если меньше — плосковершинное распределение статистического ряда. В этом случае мы наблюдаем «островершинное» распределение остатков. С более подробной интерпретацией описательной статистики можно познакомиться ниже.
Дадим некоторые пояснения к табл. 4.5. Так, среднее (Mean) равно сумме всех остатков, деленной на количество наблюдений. В свою очередь медиана (Median) представляет собой величину, расположенную в середине нечетного ряда, ранжированного в порядке возрастания или убывания. В четном ряде медиана равна среднему значению двух соседних величин, расположенных в середине ряда. Соответственно максимум (Maximum) и минимум (Minimum) означают максимальное и минимальное значения временного ряда.
Стандартное отклонение является мерой дисперсии для временного ряда и находится по формуле для стандартного отклонения по выборке:
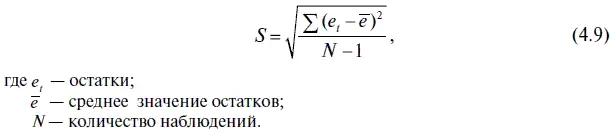
В нашем случае стандартное отклонение имеет следующее значение:
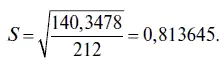
Коэффициент асимметрии является своего рода индикатором, показывающим степень асимметричности распределения статистического ряда. Следует иметь в виду, что в случае полной симметрии, в том числе и при нормальном распределении, коэффициент асимметрии должен быть равен нулю. Если коэффициент асимметрии меньше нуля, то говорят о левосторонней асимметрии, а если больше нуля, — то о правосторонней асимметрии. Коэффициент асимметрии для остатков в EViews рассчитан по следующей формуле:
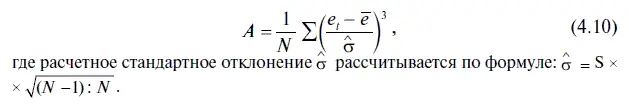
В этом случае коэффициент асимметрии имеет следующее значение:
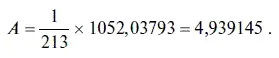
Как мы видим, в этом случае коэффициент асимметрии равен 4,939145, следовательно, в распределении остатков наблюдается очень сильная правосторонняя асимметрия, т. е. имеет место преобладание положительных остатков над отрицательными. Отсюда можно сделать вывод, что в динамике курса доллара к рублю чаще наблюдались резкие (вполне очевидно, что незначительные плавные колебания курса легко поддаются прогнозированию) подъемы, чем аналогичные падения. С фундаментальной точки зрения этот факт объясняется многолетней политикой Банка России по поддержанию слабого курса рубля.
Коэффициент эксцесса можно назвать индикатором «крутизны» распределения статистического ряда. Коэффициент эксцесса для нормального распределения равен 3. В том случае, когда этот коэффициент больше 3, это является показателем «островершинного» распределения, а если меньше 3, это свидетельствует о «плосковершинном» распределении статистического ряда. Коэффициент эксцесса для остатков в EViews вычислен по следующей формуле:
Читать дальше
Конец ознакомительного отрывка
Купить книгу