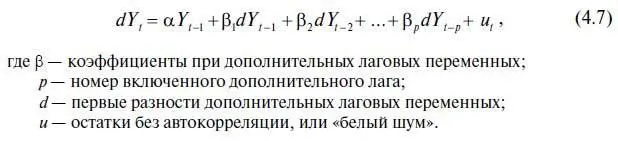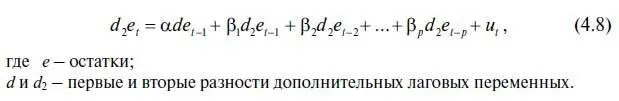Владимир Брюков - Как предсказать курс доллара. Эффективные методы прогнозирования с использованием Excel и EViews

В основе теории единичного корня лежит довольно простая формула, которая считается базовой для понимания стационарности в уравнениях авторегрессии:

Y t= ρY t- 1 + e t, (4.4)

где Y t— результативная зависимая переменная;

Y t- 1— независимая факторная переменная с лагом в один период (в нашем случае в один месяц);

ρ — коэффициент регрессии;

е t— остатки.

Уравнение авторегрессии 1-го порядка считается стационарным в том случае, когда коэффициент регрессии ρ < 1. Соответственно если ρ > 1, то оно считается нестационарным, а следовательно, волатильность с течением времени может нарастать и стремиться к бесконечности. Следует заметить, что при необходимости в формулу (4.4) может быть добавлена константа либо константа и тренд, если, конечно, они будут статистически значимыми.

Проверка авторегрессионного процесса на стационарность проводится следующим образом. Согласно нулевой гипотезе, предполагается, что если ρ = 1, то временной ряд нестационарный, а в случае ее опровержения принимается альтернативная гипотеза, утверждающая, что ρ < 1, а следовательно, ряд стационарный.

В ходе решения обычного уравнения регрессии рассчитывается t -статистика для коэффициента регрессии ρ, совпадающая с расчетными значениями статистики Дикки — Фуллера, которая потом сравнивается с критическими значениями статистики Дикки — Фуллера (обычно даются в таблице, но в EViews, естественно, мы их получим в готовом виде). Сравнение проводится по одностороннему критерию, но если бы альтернативная гипотеза состояла в утверждении, что ρ ≠ 1, то тогда мы пользовались бы двусторонним критерием. Поскольку проверка гипотезы проводится по одностороннему критерию, то в этом случае, если расчетное значение t -статистики для коэффициента регрессии ρ будет меньше критического значения статистики Дикки — Фуллера (с поправкой на число наблюдений), нулевая гипотеза о том, что ρ = 1 отклоняется и принимается альтернативная гипотеза о том, что ρ < 1, а следовательно, временн о й ряд Y t можно считать стационарным.

Стандартный тест Дикки — Фуллера проводится после вычитания Y t- 1из левой и правой частей уравнения (4.4). В результате мы получаем следующую формулу:

Y t— Y t -1= ρ Y t -1— Y t -1+ e t (4.5)

Учитывая, что dY 1 = Y t- Y t- l, а ρ Y t -1— Y t -1= (ρ -1) Y t -1, и приравняв α = (ρ-1), получим новое уравнение:

dY 1= α Y t -1+ e t (4.6)

С учетом того, что при r = 1 параметр а становится равным нулю, то соответственно в случае принятия нулевой гипотезы α = 0, а если принимается альтернативная гипотеза, то соответственно |α| < 1, а следовательно, временн о й ряд считается стационарным.

Однако на практике б о льшую популярность приобрел расширенный тест Дикки — Фуллера AUGMENTED DICKEY — FULLER, так как он учитывает возможную автокорреляцию в остатках. При этом в правую часть уравнения (4.6) включаются дополнительные лаговые переменные Y. В результате это уравнение приобретает следующий вид:

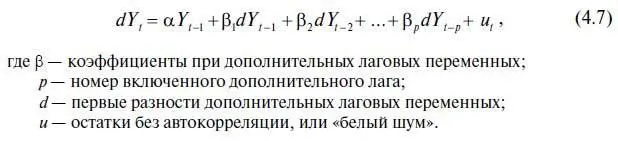
В дальнейшем эти знания нам потребуются для проверки авторегрессионного процесса 2-го порядка (см. уравнение (4.1)) на стационарность, а пока применим эту теорию для проверки на стационарность остатков, полученных в результате решения этого уравнения. Заполнив в алгоритме № 9 мини-окно UNIT ROOT TEST и щелкнув кнопку ОК, мы фактически решили следующее уравнение регрессии:

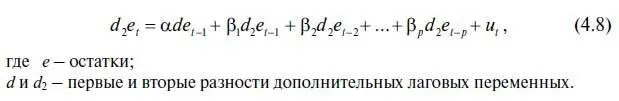
В результате решения расширенного теста Дикки — Фуллера мы получили табл. 4.4 с итогами теста, свидетельствующими о стационарности остатков. О том, как мы пришли к этому выводу, подробно рассказано выше (см. алгоритм действий № 9 «Как проверить в EViews остатки на стационарность модели»).

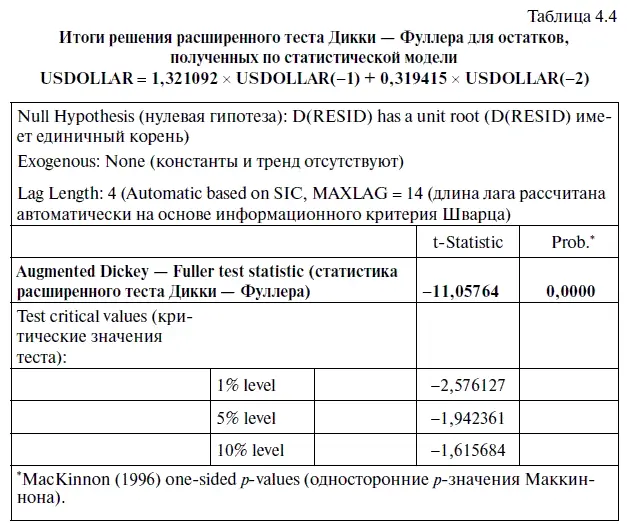
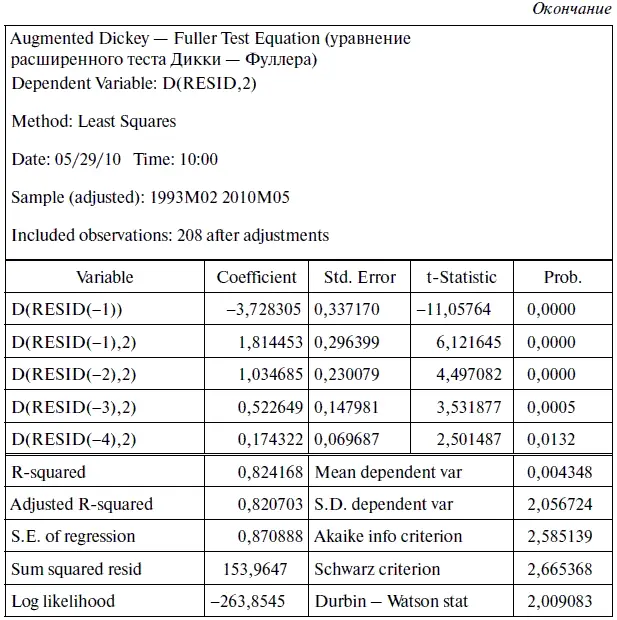
Поскольку мы доказали, что остатки, полученные по модели авторегрессии 2-го порядка без константы, являются стационарными, то, следовательно, можно сделать вывод, что их распределение носит устойчивый характер.