Эдвардс Деминг - Выход из кризиса. Новая парадигма управления людьми, системами и процессами

По поводу воспроизводимости существует много неправильных рекомендаций. Абсолютно неверно, например, взять какое-то число изделий, например 8, 20, 50 или 100, измерить их и использовать 6 стандартных отклонений, полученных по этим измерениям, в качестве меры воспроизводимости процесса. Первым шагом должен быть анализ данных с помощью карты хода процесса (глава 1) или с помощью x – и R -карт с целью решить, демонстрируют ли процесс производства и система измерений статистическую управляемость. Если да, тогда воспроизводимость процесса будет очевидна из x – и R -карт. Если нет, тогда воспроизводимости не существует.

Преимущества стабильности или статистической управляемости. Процесс, который стабилен и находится в статистически управляемом состоянии, обладает рядом преимуществ по сравнению с нестабильным процессом. При наличии статистической управляемости:

1. Процесс индивидуален, его результаты предсказуемы. Он измерим, может быть охарактеризован имеющими рациональный смысл показателями воспроизводимости, как мы видели в предыдущем разделе. Производительность, объем и другие характеристики качества, включая число дефектов, если они есть, остаются почти постоянными час за часом, день за днем.

2. Затраты предсказуемы.

3. Регулярность выхода – важный побочный продукт состояния статистической управляемости. Поставка деталей по системе канбан – следующий естественный шаг, после того как вся система приведена в статистически управляемое состояние (Уильям Шеркенбах).

4. Производительность достигает максимума (затраты минимальны) в рамках действующей системы.

5. Взаимоотношения с продавцами, поставляющими материалы, находящиеся в состоянии статистической управляемости, чрезвычайно упрощаются. Затраты снижаются по мере того, как улучшается качество.

6. Влияние изменений в системе (ответственность менеджмента) может быть измерено с большей оперативностью и надежностью. Если система не находится в состоянии статистической управляемости, трудно измерить эффект от изменений. Говоря точнее, если нет управляемости, заметны будут только катастрофические результаты.

7. Для минимизации полной стоимости затрат на контроль изделий, поступающих из статистически управляемого процесса, можно использовать правила главы 14 (контролируем все или ничего).

Согласование показаний измерительных приборов (вопрос, тесно связанный со статистической управляемостью инструментов и калибров).Этот процесс важен как для потребителей, так и для поставщиков, иначе покупателю придется переплачивать за материал или продавец может получить слишком маленькую прибыль. Оба имеют право на честную сделку. Этот процесс также важен для компании, имеющей несколько заводов по производству одной и той же или аналогичной продукции.

Другой пример использования контрольной карты для выработки суждения. Некоторые примеры вы найдете в главе 1. Теперь обратимся к другим. Исполнительный директор крупной компании, рассылающей товары по почте, обратился ко мне с просьбой разобраться с проблемой высоких затрат. Он также принес данные о числе выполненных заказов за каждые полчаса. Данные для x – и R -карты собираются каждые полчаса (рис. 36), n = 4. Как только он увидел, насколько широки оказались контрольные пределы для заказов, он заявил, что предпочитает меньшее значение вариаций. Я спросил, как они хотят этого достичь. Он предположил, что надо всего лишь нарисовать новые линии поближе друг к другу. Мне пришлось указать ему на то, что контрольные пределы всего лишь свидетельствуют о состоянии процесса, а не говорят о том, каким он может стать, и что любое снижение вариаций в будущем всецело лежит на нем. Он должен исследовать возможные общие причины вариаций и устранить их. Даже минимальный успех в этом деле повысил бы производительность и привел бы к уменьшению размаха между контрольными пределами. А это как раз то, что он хотел.

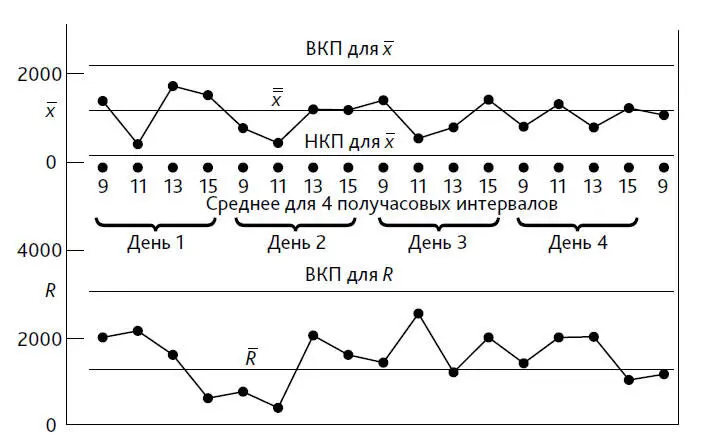
Рис. 36. Число выполненных заказов регистрируется каждые полчаса. Каждая точка на карте (результат четырех последовательных измерений) – это среднее число заказов, выполненных за четыре последовательных получасовых периода; R – это размах между этими четырьмя числами. Контрольные пределы вычисляются по обычным формулам: