Neal Stephenson - Peanatema

— Czyli samą butelkę opisujemy pięcioma liczbami — podsumował Barb.

— Właściwie dla pełnego uogólnienia przydałoby się sześć, żeby zachować informację o jej przesunięciu w pionie. — Podniosłem butelkę. — Jak widzisz, potrzebne nam jest sześć wymiarów przestrzeni konfiguracyjnej, żeby przedstawić położenie i orientację butelki. — Odłożyłem butelkę na podłogę. — Ale jeśli nie będziemy jej podnosić, wystarczy pięć.

— Rozumiem — powiedział Barb. Mówił tak tylko wtedy, kiedy naprawdę wszystko było dla niego jasne.

— Cieszę się, że tak uważasz. Rozumowanie w sześciu wymiarach nie jest proste.

— Będę miał po prostu sześć kolumn liczb na tabliczce zamiast trzech. Nie rozumiem tylko, dlaczego do opisania ziemniaka potrzebujemy sześciu nowych wymiarów. Nie moglibyśmy po prostu wykorzystać tych od butelki?

— W pewnym sensie tak właśnie robimy, tylko zapisujemy wartości w osobnych kolumnach. Dzięki temu jeden wiersz tabeli w pełni opisuje układ ziemniak-butelka w danym momencie; każdy taki wiersz, czyli ciąg dwunastu liczb — x, y i z butelki, kąt obrotu po kopnięciu, kąt obrotu do odczytania etykiety oraz kąt podniesienia nad podłogę — to jeden punkt w dwunastowymiarowej przestrzeni konfiguracyjnej. Jej przydatność dla teorów staje się oczywista, kiedy łączymy takie punkty, tworząc w niej trajektorie.

— Trajektoria kojarzy mi się z czymś, co lata w powietrzu — wtrącił Barb. — Nie bardzo rozumiem, czym miałaby być trajektoria w tej dwunastowymiarowej przestrzeni, która wcale przestrzeni nie przypomina.

— Uprośćmy sprawę maksymalnie — zaproponowałem. — Ograniczmy ruch do osi x i darujmy sobie obroty.

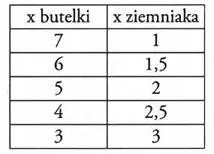
Ułożyłem ziemniak i butelkę w taki sposób:

— Możesz zapisać na tabliczce ich pozycje? — poprosiłem.

— Się robi — odparł Barb i po chwili pokazał mi coś takiego:

— Zrobimy teraz małe zderzenie — zapowiedziałem. — W zwolnionym tempie, rzecz jasna. Zapisuj położenie, z łaski swojej.

Podobnie jak chwilę wcześniej, zacząłem po kawałku przesuwać butelkę i ziemniak, pokrzykując „Teraz!” za każdym razem, kiedy chciałem, żeby Barb dodał nowy wiersz w tabeli.

— Butelka przemieszcza się szybciej — zauważył Barb.

— To prawda. Dwa razy szybciej.

Zatrzymałem ziemniak na butelce w pozycji 3.

— Zderzyły się — powiedziałem. — Teraz się odbiją, ale będą się poruszać wolniej, ponieważ ziemniak się rozpłaszczył i część energii została stracona.

Z moją małą pomocą Barb wypełnił tabelkę w taki oto sposób:

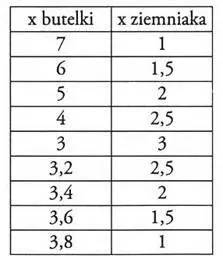
— Proszę bardzo. — Odłożyłem oba pociski i wstałem. — Całe to zderzenie odbyło się na linii prostej. Gdyby cofnąć się do współrzędnych saunta Lespera, można by powiedzieć, że mamy sytuację jednowymiarową. Natomiast saunt Hemn proponuje w tym miejscu woltę, która może ci się wydać dziwna: dla niego każdy wiersz tej tabeli określa punkt w dwuwymiarowej przestrzeni konfiguracyjnej.

— Każdą parę liczb traktuje jak punkt — przełożył to sobie Barb. — Zaczynając od (7,1).

— Zgadza się. Możesz to narysować?

— Pewnie. To banalnie proste.

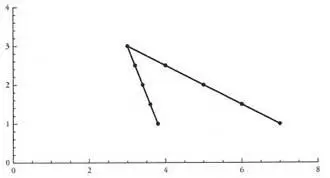
— Jakie to dziwne! — wykrzyknął Barb. — Tak jakby saun Hemn wywrócił całą tę sytuację na nice!

— Daj kredę. Dorobię opis, który pomoże ci to zrozumieć.

Chwilę później patrzyliśmy na coś takiego:

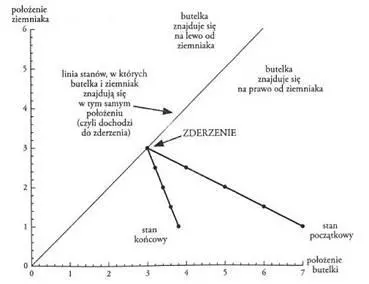
— Linia zderzeń jest zbiorem stanów, w których butelka i ziemniak znajdują się w tym samym miejscu, czyli mają takie same współrzędne — tłumaczyłem. — Każdy teor, który zobaczyłby ten wykres, stwierdziłby, że jest to linia szczególna, nawet gdyby nie miał pojęcia o całym układzie, którym się zajmujemy: butelce, ziemniaku i podłodze. Stan układu zmienia się w sposób uporządkowany i przewidywalny do momentu zetknięcia z tą linią, kiedy to dzieje się coś niezwykłego. Trajektoria gwałtownie zakręca. Tworzące ją punkty zagęszczają się, co oznacza, że obiekty poruszają się wolniej, a to z kolei świadczy o tym, że wytraciły część energii. Nie jest to pewnie szczególnie zaskakujące wnioskowanie, ale może teraz zrozumiesz, dlaczego teorowie, rozważając układy fizyczne, chętnie umieszczają je w przestrzeniach konfiguracyjnych.

— Ale to chyba nie koniec? Mogliśmy narysować to wszystko jakoś prościej, nie?

— To już jest prościej — odparłem. — Bliżej prawdy.

— Mówisz o Hylaejskim Świecie Teorycznym? — spytał Barb konspiracyjnym szeptem, jakby dyskusja o HŚT była największym bezeceństwem, jakiego fraa może się dopuścić.

— Jestem edharczykiem. Bez względu na to, co o tym myślą różni ludzie… jestem edharczykiem i koniec. To dla nas naturalne, że staramy się wyrazić nasze myśli w sposób możliwie najprostszy i najelegantszy. W wielu sytuacjach… Nie, inaczej: w większości sytuacji, które teorom wydają się interesujące, przestrzeń konfiguracyjna saunta Hemna nadaje się do tego lepiej niż przestrzeń saunta Lespera z trzema współrzędnymi x, y i z, w której do tej pory zmuszony byłeś się poruszać.

Barb doznał małego olśnienia.

— Butelkę i ziemniak opisywało sześć liczb… Sześć współrzędnych w przestrzeni Hemna.

— Zgadza się. Przedstawienie położenia obiektu zwykle wymaga sześciu liczb.

— Tak samo jak satelity na orbicie!

— Owszem: jest sześć elementów orbitalnych. Opis satelity zawsze wymaga sześciowymiarowej przestrzeni Hemna, bez względu na użyty układ współrzędnych. Jeśli posłużysz się współrzędnymi saunta Lespera, napotkasz problemy, na które niedawno się skarżyłeś…

— Że te wszystkie iksy, igreki i zety tak naprawdę nic mi nie mówią!

— No właśnie. Wystarczy jednak przenieść satelitę do innej przestrzeni sześciowymiarowej, z innym układem sześciu współrzędnych, żeby opis nagle stał się klarowny. Tak jak zagadnienie butelki i ziemniaka uprościło się, kiedy wybraliśmy dla niego odpowiednią przestrzeń. W wypadku satelity te sześć liczb to mimośród, inklinacja, argument szerokości perycentrum… i trzy inne; też mają skomplikowane nazwy i nie ma potrzeby teraz ich tu przytaczać. W każdym razie mimośród pozwala od razu stwierdzić, czy orbita jest stabilna; inklinacja informuje cię, czy jest orbitą biegunową, czy równikową. I tak dalej.

— Oto diagram z dwoma prostokątami, który wszyscy dobrze znamy — zaczął Criscan i narysował na ziemi taki rysunek: