Neal Stephenson - Peanatema

— Nie wiem.

— Pomalutku. Składa się z czterech trójkątów, tak?

— Tak.

— Każdy z tych trójkątów jest połówką małego kwadratu, tak?

— Tak.

— Ile porcji zawiera mały kwadrat?

— Cztery.

— Czyli w każdym trójkącie jest ciasta na ile porcji?

— Na dwie.

— Zatem kwadrat złożony z czterech takich trójkątów zawiera ciasta na…

— Osiem porcji. — Dath doznał olśnienia. — I to jest rozwiązanie, którego przed chwilą szukaliśmy!

— I do którego cały czas dążyliśmy. Możesz nam ukroić osiem porcji?

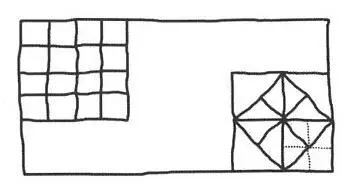
— Bardzo ładnie — pochwaliłem.

— Możemy już jeść?

— Tak. Rozumiesz, co się stało?

— No… ukroiłem osiem porcji ciasta.

— Kiedy tak mówisz, brzmi to prosto… ale wcale takie proste nie było. Przypomnij sobie: parę minut temu wiedziałeś, jak ukroić cztery porcje; to było łatwe. Wiedziałeś również, jak ukroić szesnaście. Dziewięć też. Nie umiałeś ukroić ośmiu takich porcji; wydawało się to niemożliwe. A jednak wystarczyło chwilę się zastanowić, żeby uzyskać odpowiedź, i to nie przybliżoną, tylko najzupełniej dokładną.

Tak się złożyło, że kręcąc się po kuchni, przewróciliśmy stojącą na podłodze butelkę po winie:

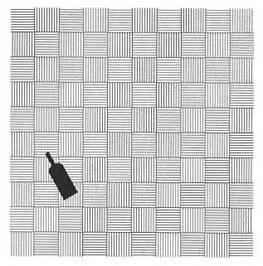
Podłoga była wykładana drewnianymi płytkami ułożonymi w kwadratowy wzór, który przywodził na myśl płaszczyznę z układem współrzędnych.

— Przynieś tabliczkę i kawałek kredy — powiedziałem do Barba.

Miałem lekkie wyrzuty sumienia, że tak mu rozkazuję, ale byłem na niego trochę zły, że nie pomógł mi przy przetykaniu odpływu. Zresztą nie miał chyba nic przeciwko temu, a spełnienie mojej prośby nie kosztowało go wiele wysiłku, bo tabliczki i kreda walały się po całej kuchni: używaliśmy ich do notowania przepisów i spisywania składników potraw.

— Bądź tak miły i zapisz współrzędne tej butelki.

— Współrzędne?

— Tak. Wyobraź sobie, że ten wzór na podłodze to układ współrzędnych saunta Lespera: każdy kwadrat to jedna jednostka. Położę ziemniak na przecięciu linii, to będzie początek układu.

— W takim razie współrzędne butelki to w przybliżeniu (2,3) — stwierdził Barb.

Wziął do ręki kredę, coś nagryzmolił na tabliczce i pokazał mi ją.

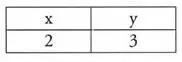
— Proszę bardzo: oto przestrzeń konfiguracyjna, chyba najprostsza, jaką można sobie wyobrazić — powiedziałem. — Położenie butelki, (2,3), jest punktem w tej przestrzeni.

— Niczym się nie różni od zwykłej przestrzeni dwuwymiarowej — poskarżył się Barb. — Nie mogłeś tak od razu powiedzieć?

— Możesz dopisać jeszcze jedną kolumnę?

— Pewnie.

— Zauważ, że butelka nie leży prosto: jest obrócona mniej więcej o dziesiątą część pi, albo w jednostkach, do których jesteście przyzwyczajeni extramuros, o jakieś dwadzieścia stopni. Wielkość obrotu będzie trzecią współrzędną w naszej przestrzeni konfiguracyjnej. Po to właśnie jest ta trzecia kolumna.

Barb pochylił się nad tabliczką i wyprodukował, co następuje:

— No tak… — przyznał. — Teraz wygląda już trochę inaczej niż stara, dobra przestrzeń dwuwymiarowa, prawda? Ma trzy wymiary, w dodatku ten trzeci jest trochę udziwniony. Kiedyś w suwinie uczyłem się o czymś podobnym…

— O współrzędnych biegunowych? — zapytałem z podziwem.

Quin musiał nieźle się wykosztować, bo posłał syna do naprawdę porządnego suwinu.

— Tak! Tam też był kąt zamiast długości.

— No dobrze. Sprawdźmy teraz, jak się ta przestrzeń zachowuje. Będę przesuwał butelkę, a kiedy powiem „teraz”, będziesz zaznaczał jej kolejne pozycje.

Przesunąłem butelkę i trochę ją obróciłem.

— Teraz.

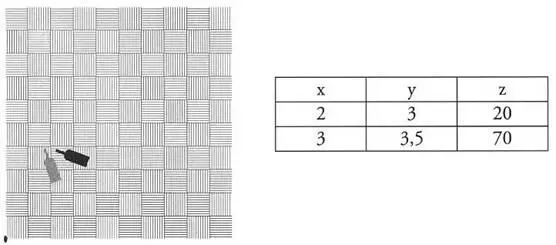
— Teraz. Teraz. Teraz…

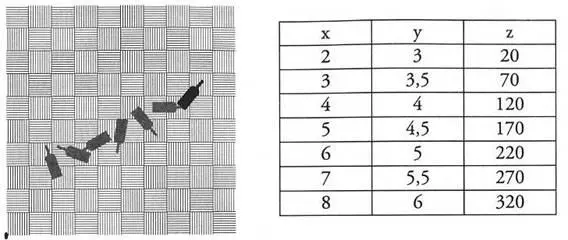
— Taki zbiór punktów w przestrzeni konfiguracyjnej uzyskałbym po przypadkowym kopnięciu butelki, która obracając się, ślizgałaby się na podłodze. Zgodzisz się ze mną?

— No jasne, sam o czymś takim pomyślałem.

— Poruszałem nią w zwolnionym tempie, żebyś nadążył z rejestracją danych.

Barb nie bardzo wiedział, jak zareagować na tę słabiutką namiastkę żartu, więc po chwili niezręcznego milczenia mówiłem dalej:

— Mógłbyś zrobić wykres tych punktów? Trójwymiarowy?

— Oczywiście — przytaknął bez przekonania Barb. — Ale będzie trochę dziwny…

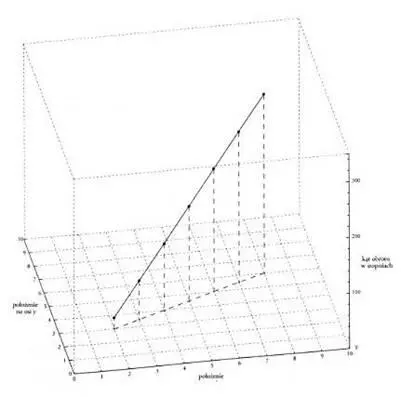
— Linia przerywana na dole ilustruje zmiany położenia butelki w płaszczyźnie (x,y) — wyjaśnił. — Jej ślad na podłodze.

— Rozumiem. Dobrze, że to zaznaczyłeś; w przeciwnym razie dla osoby nieobeznanej z przestrzenią konfiguracyjną mogłoby to być trochę niejasne. Ta część, trajektoria butelki w płaszczyźnie podłogi, zaznaczona linią przerywaną, to nic nowego: znamy takie rysunki ze zwykłej przestrzeni adrakhonejskiej. Za to nasz trzeci wymiar, kąt, to zupełnie inna historia. Nie pokazuje odległości w przestrzeni, tylko przemieszczenie kątowe butelki, inaczej mówiąc: jej obrót. Kiedy już to zrozumiesz, możesz tę informację odczytać z wykresu i powiedzieć: „No tak, zaczęła od dwudziestu stopni i ślizgając się po podłodze, doszła z obrotem do ponad trzystu”. Jednak dopóki nie znasz tego szyfru, wykres jest dla ciebie bezużyteczny.

— A do czego może być użyteczny?

— Wyobraź sobie, że zagadnienie jest bardziej skomplikowane niż butelka na podłodze. Powiedzmy, że dołączy do niej ziemniak. Wtedy do opisania stanu układu ziemniak-butelka będziesz potrzebował dziesięciowymiarowej przestrzeni konfiguracyjnej.

— Dziesięciowymiarowej?!

— Pięć dla butelki, pięć dla ziemniaka.

— Ale dlaczego pięć? Do opisu butelki wystarczyły nam trzy!

— Tylko dlatego, że trochę oszukujemy. Pomijamy dwa rotacyjne stopnie swobody.

— To znaczy…?

Przykucnąłem i wziąłem butelkę do ręki. Leżała zwrócona etykietą do ziemi. Odwróciłem ją.

— Widzisz? Obracam ją wokół osi, żeby odczytać etykietkę. Taki obrót jest całkowicie niezależny od obrotów wywołanych kopnięciem. Dlatego potrzebujemy dodatkowego wymiaru, żeby go zapisać. Przybywa nam jedna kolumna na tabliczce. — Chwyciłem butelkę za szyjkę i przyciskając denko do podłogi, podniosłem ją skośnie, jak miniaturową armatę. — A to kolejny przykład niezależnego obrotu.